数列（その2）【大学入学共通テスト2021年数学ⅡB】

2023年2月16日大学入学共通テスト,数列

\( \ a_n=3n \ \) , \( \ b_n=3\cdot 2^{n-1} \ \) であるから、
\( \ \displaystyle\sum_{k=1}^{n}{a_k}=\displaystyle\frac{{\color{#0004fc}{3}}}{{\color{#0004fc}{2}}}n\left( n+{\color{#0004fc}{1}}\right) \ \)
\( \ \displaystyle\sum_{k=1}^{n}{b_k}={\color{#0004fc}{3}}\left( 2^n-{\color{#0004fc}{1}}\right) \ \)

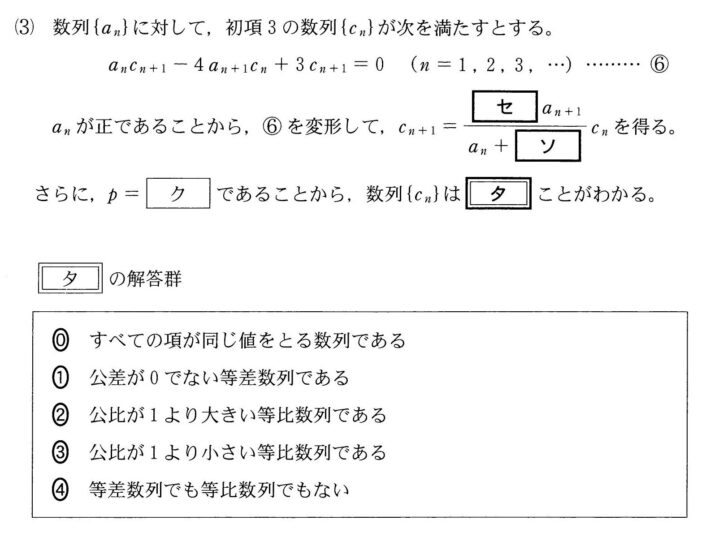$$\begin{align}\left( 3+a_n\right)c_{n+1}=&4a_{n+1}c_n \\\\ c_{n+1}=&\frac{{\color{#0004fc}{4}}a_{n+1}}{a_n+{\color{#0004fc}{3}}}c_n \end{align}$$ さらに
$$\begin{align}c_{n+1}=&\frac{4a_{n+1}}{a_n+3} \\\\ =&\frac{4a_{n+1}}{a_{n+1}} \\\\ =&4c_n \end{align}$$
\( \ c_n \ \) は公比 \( \ 4 \ \) の等比数列であるとわかる。
ゆえに選択肢② 「公比が \( \ 1 \ \) より大きい等比数列である」

以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。

大学入学共通テスト2021年数学ⅡBの記事一覧

2021年大学入学共通テストの数学2Bの問題を解いてみました。

 https://makelemonadejp.com/common-test-for-university-admiss...

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。