正十二面体とベクトル（その2）【大学入学共通テスト】
読了時間: 約1分9秒
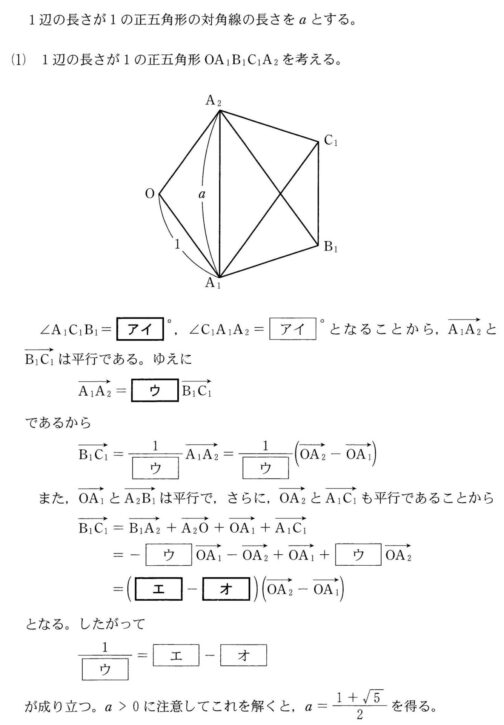
誘導により
\( \ \overrightarrow{\mathrm{B_1C_1}}=\displaystyle\frac{1}{a}\left( \overrightarrow{\mathrm{OA_2}}-\overrightarrow{\mathrm{OA_1}}\right) \ \)
さらに誘導により
\( \ \overrightarrow{\mathrm{B_1C_1}}=-a\overrightarrow{\mathrm{OA_1}}-\overrightarrow{\mathrm{OA_2}}+\overrightarrow{\mathrm{OA_1}}+a\overrightarrow{\mathrm{OA_2}} \ \)
\( \ {\color{#ffffff}{\overrightarrow{\mathrm{B_1C_1}}}}=\left( {\color{#0004fc}{a}}-{\color{#0004fc}{1}}\right)\left( \overrightarrow{\mathrm{OA_2}}-\overrightarrow{\mathrm{OA_1}}\right) \ \)
\( \ {\color{#ffffff}{\overrightarrow{\mathrm{B_1C_1}}}}=\left( {\color{#0004fc}{a}}-{\color{#0004fc}{1}}\right)\left( \overrightarrow{\mathrm{OA_2}}-\overrightarrow{\mathrm{OA_1}}\right) \ \)
となる。したがって
\( \ \displaystyle\frac{1}{a}=a-1 \ \) が成り立つ。
ここで、近いうちに役に立つかもしれないので、上記の式を変形しておく。
$$\begin{align}\frac{1}{a}=&a-1 \\ \\ 1=&a^2-a \\ a^2=&a+1 \end{align}$$
以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。
https://makelemonadejp.com/common-test-for-university-admiss...共有:
プロフィール
Author Profile
