三角関数の最大値（その2）【大学入学共通テスト2021年数学ⅡB】

2023年2月9日三角関数,大学入学共通テスト

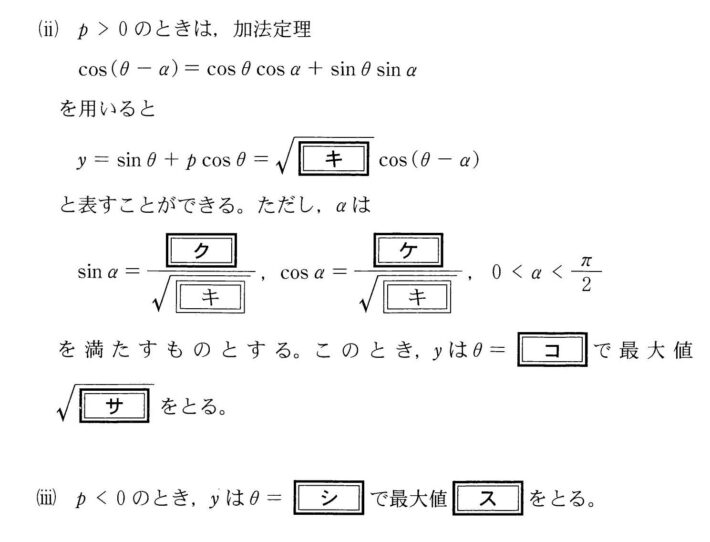
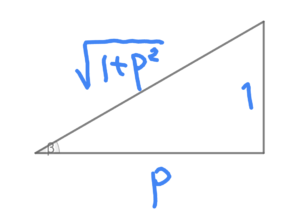
\( \ y=\sqrt{{\color{#0004fc}{1+p^2}}}\cos \left( \theta-\alpha\right) \quad \left( -\alpha \leqq \theta-\alpha \leqq \displaystyle\frac{ \pi }{ 2 }-\alpha\right) \ \)
ただし \( \ \alpha \ \) は、\( \ \sin \alpha=\displaystyle\frac{{\color{#0004fc}{1}}}{\sqrt{{\color{#0004fc}{1+p^2}}}} \ , \ \cos \alpha=\displaystyle\frac{{\color{#0004fc}{p}}}{\sqrt{{\color{#0004fc}{1+p^2}}}} \ \) を満たす。
（ \( \ \alpha \ \) は鋭角 ）

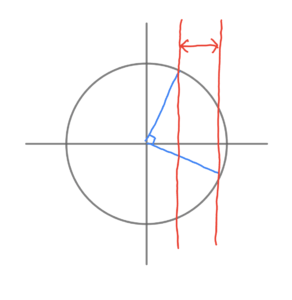\( \ \theta-\alpha=0 \ \) すなわち、\( \ \theta=\alpha \ \) のとき、
\( \ y=\sqrt{1+p^2}\times 1 \ \)
最大値は \( \ {\color{#0004fc}{\sqrt{1+p^2}}} \ \) をとる。

\( \ p \lt 0 \ \) のとき、 \( \ \alpha \ \) は鈍角であるから、
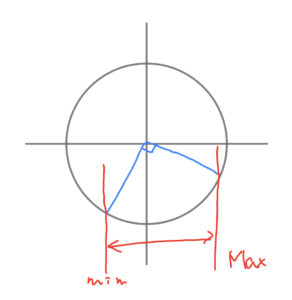\( \ \theta-\alpha=\displaystyle\frac{ \pi }{ 2 }-\alpha \ \) すなわち、\( \ \theta=\displaystyle{\color{#0004fc}{\frac{ \pi }{ 2 }}} \ \) のとき、
$$\begin{align}y=&\sqrt{1+p^2}\cos \left( \frac{ \pi }{ 2 }-\alpha\right) \\\\ =&\sqrt{1+p^2}\lbrace \cos \frac{ \pi }{ 2 }\cos \alpha+\sin \frac{ \pi }{ 2 }\sin \alpha\rbrace \\\\ =&\sqrt{1+p^2}\times \frac{1}{\sqrt{1+p^2}}={\color{#0004fc}{1}} \end{align}$$

以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。

大学入学共通テスト2021年数学ⅡBの記事一覧

2021年大学入学共通テストの数学2Bの問題を解いてみました。

 https://makelemonadejp.com/common-test-for-university-admiss...

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。