立式いろいろ・グラフもいろいろ【ビジネス数学検定2級合格への道】

2022年5月28日2023年1月31日ビジネス数学検定ビジネス数学検定2級

読了時間: 約4分16秒

第75回ビジネス数学検定受検まであと31日
受検勉強を再開した2022年4月18日より41日経過しています。

問題

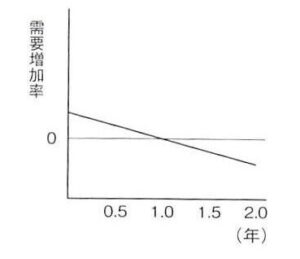
ある企業で新商品の需要増加率をシミュレーション予測したところ、以下のようなグラフの結果が得られた。

この需要増加率のデータを基に今後の商品需要量を予測したとき、需要量の傾向を示すグラフを選べ。
（選択肢のグラフは省略）

積分すればいいんじゃない？

答えは図のような放物線を描きます。

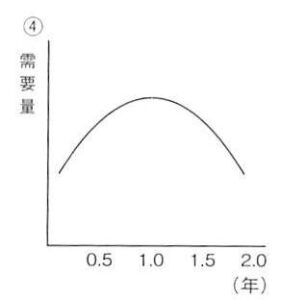
これまではしっかり理解できたわけではないけれど、元が右下がりの一次関数なので、まぁ、該当するならこれかなぁ。というレベルで放物線を選んでいました。

ところが、今朝方、まどろみの中であるアイディアが浮かびます。
ワクチン接種した左腕が傷まないように気を遣って寝ていたのか、眠りが浅かったのでしょう。
途中で考えるのをやめていたことがあれこれ浮かんできました。

この形式の問題で、右下がりの直線のグラフが出れば何も考えず上に凸の放物線を選べばいいんだろうけれど、
なにか理屈はないのか。と思っていました。

すると、ふと、思いつく。

Lukia

二次関数を微分すれば、一次関数が出るよね。

たしかに。

たとえば、$ \ y=-ax^2+bx+c \ $ (ただし、$ \ a,b,c \ $は実数。特に$ \ a \gt 0 \ $）を微分すると、
$ \ y’=-ax+b \ $となります。

Lukia

うおぉ、じゃ、積分すればいいんじゃない？

と思いましたが、そう簡単でもなかったようです。

私の仮説は正しくなかった

この仮説が正しければ、需要増加率を表す関数を積分すれば、需要量の関数が求められるはずです。
しかし、解説のページを読んでいたら、
需要増加率が一定の場合は、指数関数になるという例が示されていました。
$ \ y=a \ $($ \ a \ $は正の実数）を積分すると、$ \ y=ax+\mathrm{C} \ $($ \ \mathrm{C} \ $は積分定数）となり、
指数関数にはなりません。
逆に指数関数を微分してみましたが、ビジネス数学検定に数学Ⅲレベルは必要ないはず。
つまり、私の仮説は間違っていることになります。

需要量の求め方を理解し直す

需要量の変化は、前期の需要量に需要増加率をかければ求められます。
需要増加率が$ \ y=-100x+100 \ $で表されるとします。
また、グラフの目盛りにならって、$ \ x=0.1, \ 0.2, \ 0.3, \ \cdots \ $とします。
$ \ x=0.1 \ $年のとき、
$ \ y=-100\times 0.1+100=90 \ $(%)ですが、
徐々に減っていきます。
$ \ x=0.5 \ $年（すなわち$ \ 6 \ $ヶ月経過）のとき、
$ \ y=-100\times 0.5+100=50 \ $(%)であり、
$ \ x=1.0 \ $年（すなわち$ \ 12 \ $ヶ月経過）のとき、
$ \ y=-100\times 1.0+100=0 \ $であり、
$ \ x=1.5 \ $年（すなわち$ \ 18 \ $ヶ月経過）のとき、
$ \ y=-100\times 1.5+100=-50 \ $(%)となります。

需要量を$ \ \mathrm{D}_n \ $ ($ \ \mathrm{D}_0=1 \ $,$ \ n=\displaystyle\frac{x}{0.1} \ $)とすると、 $ \ \mathrm{D}_{n+1}=\mathrm{D}_n\cdot \left( 1+\displaystyle\frac{y}{100}\right) \ $で表されることになります。

たとえば、$ \ 0.1 \ $年後の需要量は開始時の1.9倍なのですが、
増加率は徐々に減っていくので、0.2年後の需要量は、0.1年後の1.8倍となります。

$$\begin{align}\mathrm{D}_0=&1 \\\\ \mathrm{D}_1=&\mathrm{D}_0\times \left( 1+\frac{90}{100}\right)=1.9 \\\\ \mathrm{D}_2=&\mathrm{D}_1\times \left( 1+\frac{80}{100}\right)=1.9\times 1.8\\\\ &\vdots\\\\ \mathrm{D}_5=&\mathrm{D}_4\times \left( 1+\frac{50}{100}\right)=1.9\times 1.8\times 1.7\times 1.6\times 1.5\\\\ &\vdots\\\\ \mathrm{D}_{10}=&\mathrm{D}_9\times \left( 1+\frac{80}{100}\right)=1.9\times 1.8\times 1.7\times 1.6\times 1.5\times \cdots\times 1.0\\\\ \mathrm{D}_{11}=&\mathrm{D}_{10}\times \left( 1-\frac{90}{100}\right)=\mathrm{D}_{10}\times 0.9\\\\ &\vdots\\\\\mathrm{D}_{15}=&\mathrm{D}_{14}\times \left( 1-\frac{50}{100}\right)=\mathrm{D}_{14}\times 0.5\\\\ &\vdots \end{align}$$
このように増加のスピードがゆるやかになってゆき、
1.0年後には、増加も減少もしなくなります。
そして、その後、増加率がマイナス、つまり減少率が上がっていくため、需要量は減っていきます。

放物線は、頂点へ近づくほど、等間隔の区間内での傾きは徐々にゆるやかになっていきます。