損益分岐点売上高を中学数学で理解する【ビジネス数学検定2級 合格への道】
受検勉強を再開した2022年4月18日より31日経過しています。
損益分岐点売上高って何よ?!
ビジネス数学検定を勉強し始めて困ったことは、ビジネスマンなら常識である用語やその定義を知らないことでした。
定義を理解できていないものに数学の知識を応用できるわけもありません。
結局最初のうちは、公式と言葉を丸覚えするようにしていました。
しかし、丸覚えするつもりで勉強していると、徐々に言葉の意味と、数式の仕組みがわかってきます。
そして、今まで知らなかったものは、自分の知識を用いて自分なりに捉え直すことでしか理解できないようです。
見出しの「損益分岐点売上高」も一次関数や連立方程式という中学数学レベルで説明できることがわかってきました。
損益分岐点売上高は2つの直線の交点である
| 販売単価 | 変動費 （商品1個あたり） |
固定費 |
| 8000円 | 3000円 | 1600万 |
\( \ \rm{損益分岐点売上高}=\rm{販売単価}\times \displaystyle\frac{\rm{固定費}}{\rm{販売単価}-\rm{変動費}} \ \)
という言葉と公式を丸覚えするしかありませんでした。
また、下のような図があっても、いまひとつ理解できずにいました。
しかし、眺めていると中学数学で習う一次関数のグラフが用いられていること、損益分岐点売上高は、2つの直線の交点であることがわかってきて、
連立方程式で解いてみる
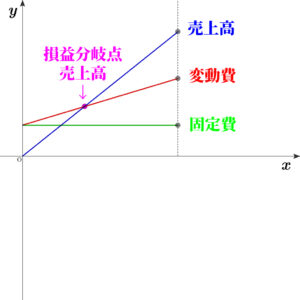\( \ x \ \)を商品を販売した個数、\( \ y \ \)を金額（万円）とする。
売上高は、\( \ y=0.8x \ \)で表せる。
\( \ \rm{営業費用}=\rm{変動費}+\rm{固定費} \ \)であるので、
営業費用は、\( \ y=0.3x+1600 \ \)で表せる。
\( \ \rm{営業利益}=\rm{売上高}-\rm{営業費用} \ \) であるが、
損益分岐点売上高では、売上高と営業費用が等しい（営業利益は出ない）といえるので、
損益分岐点売上高は、連立方程式
\begin{eqnarray} \left\{ \begin{array}{l} y = 0.8x \\ y = 0.3x+1600 \end{array} \right. \end{eqnarray}
を解くことで得られる。
$$\begin{align}\rm{損益分岐点売上高}=&0.8\times 3200 \\\\ =&2560 \end{align}$$ 求める損益分岐点売上高は\( \ 2560 \ \)万円である。
公式はいじくってみよう
勉強を始めた頃に丸覚えするしかないと思っていた
\( \ \rm{損益分岐点売上高}=\rm{販売単価}\times \displaystyle\frac{\rm{固定費}}{\rm{販売単価}-\rm{変動費}} \ \)
の公式も、上記の数式をたどっていけば理解できそうです。
公式の\( \ \displaystyle\frac{\rm{固定費}}{\rm{販売単価}-\rm{変動費}} \ \) は、実は損益分岐点売上高に至るときの販売個数でした。
この販売個数は、
$$\begin{align}0.8x=&0.3x+1600 \\\\ x=&\frac{1600}{\left( 0.8-0.3\right)} \\\\ \rm{販売個数}=&\displaystyle\frac{\rm{固定費}}{\left( \rm{販売単価}-\rm{変動費}\right)} \end{align}$$ で求められました。
毎度このように式変形するのはしんどいし、試験中に悠長なことはできませんから、
最終的には公式を覚えるべきなんでしょうけど、いきなり丸覚えしただけでは難しい問題に太刀打ちできないのも事実です。
公式としてあ〜っさり書いてあるものも、どういう理屈でそういう仕組みになったのかいじくりまわしてみるって必要だなと思いました。
ビジネス数学検定2級 合格への道の記事一覧
https://makelemonadejp.com/challenge-business-mathmatics-gra...
よろしければ,アンケートに御協力ください。
アンケートでは、お読みになったタイトルをうかがいますので、御確認ください。
この記事のタイトルは『損益分岐点売上高を中学数学で理解する』です。
共有:
プロフィール