限界利益率を求める【ビジネス数学検定2級 合格への道】

読了時間: 約2分30秒
第75回 ビジネス数学検定受検まで あと40日受検勉強を再開した2022年4月18日より32日経過しています。
問題
下の表のとき、この商品の限界利益率を求めよ。
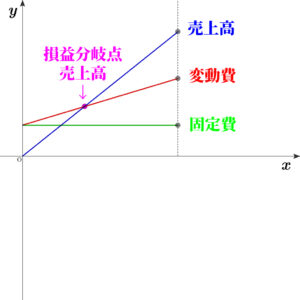
限界利益率とは、損益分岐点売上高に占める固定費の割合のこと。
| 売上高 | 販売単価 | 変動費 (商品1個あたり) |
固定費 |
| 2500万円 | 8000円 | 3000円 | 1600万円 |
準備:文字を含んだ数式で理解する
\( \ \rm{限界利益率}=\displaystyle\frac{\rm{固定費}}{\rm{損益分岐点売上高}} \ \)
$$\begin{align}\rm{営業利益}=&\rm{売上高}-\rm{営業費用} \\\\ =&\rm{売上高}-\rm{変動費}-\rm{固定費} \\\\ \rm{両辺を}&\rm{売上高で割る}\\\\ \frac{\rm{営業利益}}{\rm{売上高}}=&1-\frac{\rm{変動費}}{\rm{売上高}}-\frac{\rm{固定費}}{\rm{売上高}} \\\\\rm{上のグラフより、}&\rm{損益分岐点では} \rm{営業利益}=0 \ \rm{といえるので、}\\\\ 0=&1-\frac{\rm{変動費}}{\rm{損益分岐点売上高}}-\frac{\rm{固定費}}{\rm{損益分岐点売上高}}\\\\ 1-\frac{\rm{変動費}}{\rm{損益分岐点売上高}}=&\frac{\rm{固定費}}{\rm{損益分岐点売上高}}\\\\ \rm{限界利益率}=&\frac{\rm{固定費}}{\rm{損益分岐点売上高}} \end{align}$$
 $$\begin{align}\rm{限界利益率}=&\frac{\rm{固定費}}{\rm{損益分岐点売上高}} \\\\ =&\rm{固定費}\times \left( \frac{1}{\rm{販売単価}}\times \frac{\rm{販売単価}-\rm{変動費}}{\rm{固定費}}\right) \\\\ =&\frac{\rm{販売単価}-\rm{変動費}}{\rm{販売単価}} \end{align}$$
$$\begin{align}\rm{限界利益率}=&\frac{\rm{固定費}}{\rm{損益分岐点売上高}} \\\\ =&\rm{固定費}\times \left( \frac{1}{\rm{販売単価}}\times \frac{\rm{販売単価}-\rm{変動費}}{\rm{固定費}}\right) \\\\ =&\frac{\rm{販売単価}-\rm{変動費}}{\rm{販売単価}} \end{align}$$
解法1:損益分岐点売上高から求める
\( \ \rm{限界利益率}=\displaystyle\frac{\rm{固定費}}{\rm{損益分岐点売上高}} \ \) である。
また、\( \ \rm{損益分岐点売上高}=\rm{販売単価}\times \displaystyle\frac{\rm{固定費}}{\rm{販売単価}-\rm{変動費}} \ \)より、
$$\begin{align}\rm{損益分岐点売上高}=&0.8\times \frac{1600}{0.8-0.3} \\\\ =&2560 \end{align}$$ $$\begin{align}\rm{限界利益率}=&\frac{1600}{2560} \\\\ =&0.625 \end{align}$$
解法2:販売価格と変動費だけでも求められる
式変形することによって、
\( \ \rm{限界利益率}=\displaystyle\frac{\rm{販売単価}-\rm{変動費}}{\rm{販売単価}} \ \) と表せることから、
$$\begin{align}\rm{限界利益率}=&\frac{0.8-0.3}{0.8} \\\\ =&\frac{0.5}{0.8} \\\\ =&0.625 \end{align}$$
ビジネス数学検定2級 合格への道の記事一覧

[subscribe2]
よろしければ,アンケートに御協力ください。
アンケートでは、お読みになったタイトルをうかがいますので、御確認ください。
この記事のタイトルは『限界利益率を求める』です。











ディスカッション
コメント一覧
まだ、コメントがありません