徒歩通学の生徒は何人？【ベン図より便利!!「3つの集合」問題をカルノー図でサクッと解く】

2022年8月12日2023年1月31日SPI能力検査（非言語分野）,集合と論理3つの集合問題をカルノー図で解く,SPI能力検査(非言語分野)

「3つの集合問題は」カルノー図しか勝たん！

ベン図を用いて「3つの集合」問題を解くのは結構大変。
なぜなら、円形の集合が重なることによって、部分集合が8つもできるからです。
そこで、横3本、縦5本の線を引いて作る「カルノー図」での解法を提案します。
立式まで覚えてしまえば、ベン図よりかなり楽にサクサク解けるようになりますよ。

カルノー図？なにそれ？という方に

問題それぞれでは、集合とカルノー図との関係をあまり詳しく書いていません。
まずはこちらの記事をお読みになって、カルノー図が3つの集合をいかに簡単に整理しているかを体感してください。

解法

全体集合(生徒数)を集合\( \ \mathrm{U} \ \),
『条件\( \ \mathrm{X} \ \)(電車)』を集合\( \ \mathrm{X} \ \),
『条件\( \ \mathrm{Y} \ \)(バス)』を集合\( \ \mathrm{Y} \ \),
『条件\( \ \mathrm{Z} \ \)(自転車)』を集合\( \ \mathrm{Z} \ \)とする.

3つの集合をベン図で表すと以下の図のとおり。
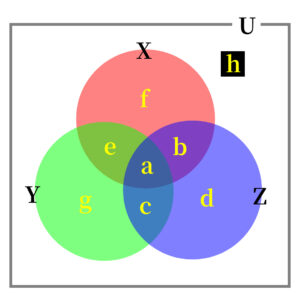横3本,縦5本の線で以下のような「カルノー図」を作成する.
（ベン図とカルノー図に示す記号\( \ a \ \)〜\( \ h \ \)は、それぞれ対応している）


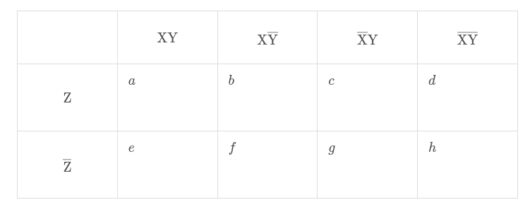
いずれの通学手段も用いない生徒の人数を\( \ x \ \)とする。

	$$\mathrm{XY}$$	$$\mathrm{X}\overline{\mathrm{Y}}$$	$$\overline{\mathrm{X}}\mathrm{Y}$$	$$\overline{\mathrm{XY}}$$
$$\mathrm{Z}$$	\( \ a \ \)	\( \ b \ \)	\( \ c \ \)	\( \ d \ \)
	$$3$$	$$5$$	$$6$$
$$\overline{\mathrm{Z}}$$	\( \ e \ \)	\( \ f \ \)	\( \ g \ \)	\( \ h \ \)
	$$4$$			$$x$$

\begin{eqnarray} \left\{ \begin{array}{l} \mathrm{U} = 40\\ \mathrm{X} =18 \\\mathrm{Y} = 15\\\mathrm{Z} =17\end{array} \right. \end{eqnarray}

\begin{eqnarray} \left\{ \begin{array}{l} \mathrm{X}+\mathrm{Y}+\mathrm{Z} =3a+2\left( b+c+e\right)+\left( d+f+g\right)=50 \\ \mathrm{X}\cup\mathrm{Y}\cup\mathrm{Z}=a+\left( b+c+e\right) + \left( d+f+g\right) =40-x \end{array} \right. \end{eqnarray}

特に, \( \ \alpha=b+c+e=15 \ \), \( \ \beta=d+f+g \ \) とする.
\begin{eqnarray} \left\{ \begin{array}{l} 3a+2\alpha+\beta =50 \quad \cdots \ ① \\ a+\alpha+\beta =40-x \quad \cdots \ ② \end{array} \right. \end{eqnarray} ①に\( \ a=3 \ \) を代入して
$$\begin{align}3a+2\alpha+\beta=&3\times 3+2\times 15+\beta=50 \\\\ \beta=&11 \end{align}$$ これらの値を②に代入して
$$\begin{align}a+\alpha+\beta=&3+15+11=40-x \\\\ x=&11 \end{align}$$

こたえ

\( \ 11 \ \)人

ほかの問題にもチャレンジ！

2022年現在、「3つの集合」問題は、全部で16問あります。
以下の一覧ページから、ほかの問題ページに飛んで、軽々解けるようになるまで練習してみてください。

Leave This Blank:Leave This Blank Too:Do Not Change This:

メールアドレス：

 

よろしければ、アンケートに御協力ください。
アンケートでは、お読みになったタイトルをうかがいますので、御確認ください。
この記事のタイトルは『徒歩通学の生徒は何人？』です。