3つの集合をカルノー図で整理する【ベン図より便利!!「3つの集合」問題をカルノー図でサクッと解く】
「3つの集合問題は」カルノー図しか勝たん！
ベン図を用いて「3つの集合」問題を解くのは結構大変。
なぜなら、円形の集合が重なることによって、部分集合が8つもできるからです。
そこで、横3本、縦5本の線を引いて作る「カルノー図」での解法を提案します。
立式まで覚えてしまえば、ベン図よりかなり楽にサクサク解けるようになりますよ。
この記事では、3つの集合とカルノー図を対応させてみます。
最終的には、以下に紹介する集合の包含関係が、ぱっと脳内変換できるようになってほしいと思います。
3つの集合とカルノー図の関係
全体集合を集合( \ \mathrm{U} \ ),
『条件( \ \mathrm{X} \ )』を集合( \ \mathrm{X} \ ),
『条件( \ \mathrm{Y} \ )』を集合( \ \mathrm{Y} \ ),
『条件( \ \mathrm{Z} \ )』を集合( \ \mathrm{Z} \ )とする.
3つの集合をベン図で表すと以下の図のとおり。
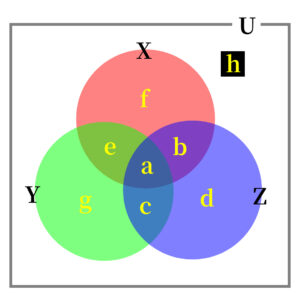横3本,縦5本の線で以下のような「カルノー図」を作成する.
（ベン図とカルノー図に示す記号( \ a \ )〜( \ h \ )は、それぞれ対応している）
単一の集合をカルノー図で表す
集合X
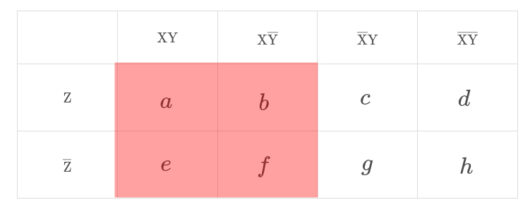集合( \ \mathrm{X} \ )は、カルノー図の赤色で塗りつぶされた部分にあたります。
$$\Large \mathrm{X}=a+b+e+f$$
集合Y
集合( \ \mathrm{Y} \ )は、カルノー図の緑色で塗りつぶされた部分にあたります。
$$\Large \mathrm{Y}=a+e+c+g$$
集合Z
集合( \ \mathrm{Z} \ )は、カルノー図の青色で塗りつぶされた部分にあたります。
$$\Large \mathrm{Z}=a+b+c+d$$
2つの集合の共通集合（積集合）をカルノー図で表す
XかつY
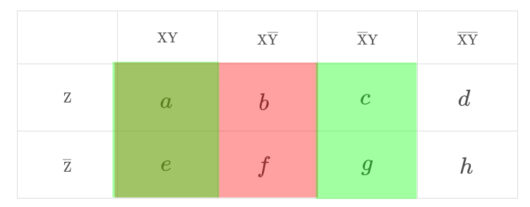集合( \ \mathrm{X}\cap\mathrm{Y} \ )は、カルノー図の赤色と緑色が混ざり、濃い緑色（モスグリーン）に塗りつぶされた部分にあたります。
$$\Large \mathrm{X}\cap\mathrm{Y}=a+e$$
YかつZ
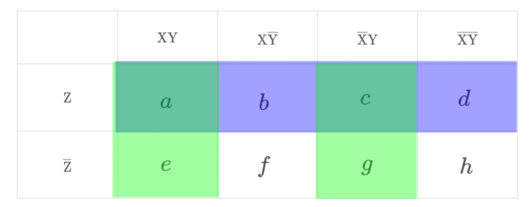集合( \ \mathrm{Y}\cap\mathrm{Z} \ )は、カルノー図の緑色と青色が混ざり、青緑色に塗りつぶされた部分にあたります。
$$\Large \mathrm{Y}\cap\mathrm{Z}=a+c$$
ZかつX
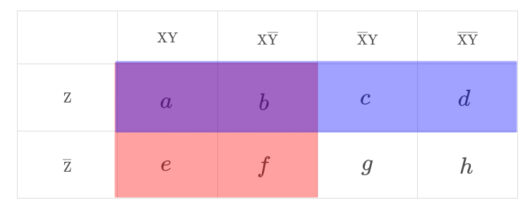集合( \ \mathrm{Z}\cap\mathrm{X} \ )は、カルノー図の青色と赤色が混ざり、紫色に塗りつぶされた部分にあたります。
$$\Large \mathrm{Z}\cap\mathrm{X}=a+b$$
2つの集合の合併集合（和集合）をカルノー図で表す
XまたはY
集合( \ \mathrm{X}\cup\mathrm{Y} \ )は、カルノー図の赤色と緑色と2色が混ざった濃い緑色（モスグリーン）に塗りつぶされた部分にあたります。
$$\Large \mathrm{X}\cup\mathrm{Y}=a+b+c+e+f+g$$
YまたはZ
集合( \ \mathrm{Y}\cup\mathrm{Z} \ )は、カルノー図の緑色と青色と2色が混ざった青緑色に塗りつぶされた部分にあたります。
$$\Large \mathrm{Y}\cup\mathrm{Z}=a+b+c+d+e+g$$
ZまたはX
集合( \ \mathrm{Z}\cup\mathrm{X} \ )は、カルノー図の青色と赤色と2色が混ざった紫色に塗りつぶされた部分にあたります。
$$\Large \mathrm{Z}\cup\mathrm{X}=a+b+c+d+e+f$$
3つの集合を足し合わせる
3つの集合を足し合わせた状態は、以下の図のようになります。
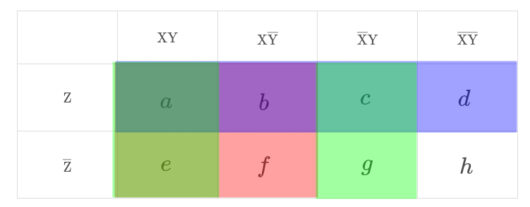しかし、この図の色を表現することは難しいので、あらためて、集合が重なり合っている数ごとに色分けをしてみます。それが以下の図です。
3つの集合が重なり合っている部分を灰色、
2つの集合が重なり合っている部分をピンク色、
1つの集合だけの部分を水色で表しています。
$$\Large \begin{align}\mathrm{X}+\mathrm{Y}+\mathrm{Z}=&\left( a+e+b+f\right)+\left( a+e+c+g\right)+\left( a+b+c+d\right) \\ =&3a+2\left( b+c+e\right)+\left( d+f+g\right) \end{align}$$
3つの集合の合併集合（和集合）をカルノー図で表す
3つの集合の合併集合（和集合）とは、「( \ \mathrm{X} \ )または( \ \mathrm{Y} \ )または( \ \mathrm{Z} \ )」のことです。
3つの集合のどこかに含まれていればいいということですので、
以下の図の黄色に塗りつぶされた部分にあたります。
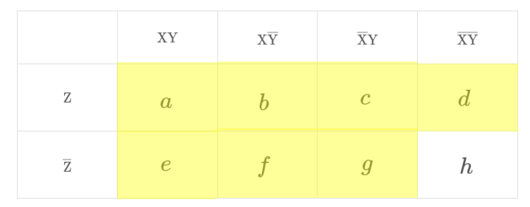$$\Large \begin{align}\mathrm{X}\cup\mathrm{Y}\cup\mathrm{Z}=&a+b+c+d+e+f+g \\ =&a+\left( b+c+e\right)+\left( d+f+g\right) \end{align}$$ また、上のカルノー図より、3つの集合の合併集合（和集合）は、全体集合( \ \mathrm{U} \ )から( \ \overline{\mathrm{X}}かつ\overline{\mathrm{Y}}かつ\overline{\mathrm{Z}} \ )、すなわち( \ h \ )を引いたものに等しいことがわかります。
$$\Large \begin{align}\mathrm{X}\cup\mathrm{Y}\cup\mathrm{Z}=&\mathrm{U}-\left( \overline{\mathrm{X}\cup\mathrm{Y}\cup\mathrm{Z}}\right) \\ =&\mathrm{U}-\left( \overline{\mathrm{X}}\cap\overline{\mathrm{Y}}\cap\overline{\mathrm{Z}}\right) \\ =&\mathrm{U}-h \end{align}$$
問題にチャレンジ！
2022年現在、「3つの集合」問題は、全部で16問あります。
以下の一覧ページから、ほかの問題ページに飛んで、軽々解けるようになるまで練習してみてください。
https://makelemonadejp.com/3sets-with-karnaugh-map-postlistよろしければ、アンケートに御協力ください。
アンケートでは、お読みになったタイトルをうかがいますので、御確認ください。
この記事のタイトルは『3つの集合をカルノー図で整理する』です。
共有:
プロフィール
