高校数学の一次不定方程式を用いれば、イチゴとマシュマロの数も数えられます。(Yahoo!知恵袋より)

2020年6月8日2023年1月13日整数の性質実用数学技能検定（数学検定 数検),数検2級,数検準2級

イチゴとマシュマロのパックの使いみちが気になって・・・

Yahoo!知恵袋でこの問題を見かけたとき、脳内には、高校数学には直結しにくいイメージが浮かびました。

Lukia

なんて、乙女チックな。。。
淡い色合いでふわっふわのマシュマロと、ビビッドな赤のイチゴ。。。
いったい、500gのそれらで何をするのか。
気になる。うおぉ、すっごく気になるぞ〜〜〜〜！

甘いものがらみといえば、絶対値の問題で登場する恐竜高校生ディノさんですが、
今回は、一次不定方程式というジャンル違いですし、彼を登場させる発想もできないほど、
イチゴとマシュマロの使いみちが気になってしかたありませんでした。(笑)

ディノ

俺の存在すら忘れるなんて、ひどいやつだぜ。

イメージは、スイートですが、問題としては意外にビターかもしれません。
「進撃！巨人中学校」のサシャとアルミンの数学に関するエピソードも思い浮かびました。
（サシャなら、問題文を読んだ時点でイチゴとマシュマロのインパクトにやられ、思考停止しちゃうでしょうね。）

Lukia

サシャの情動を持ちつつ、アルミンの理性をもって解いてみたいと思います。
ちなみに、マシュマロって、英語でmarshmallowって書くんですって。

解法

イチゴを\( \ x\ \)個、マシュマロを\( \ y\ \)個とする。
\( \ x\ \)と\( \ y\ \)はともに自然数である。

問題文より、以下のような一次不定方程式が立てられる。
\( \ 23x+12y=500\ \)

また、上の式が成立するには
少なくとも\( \ x\ \)は偶数である必要がある。

Lukia

イチゴの重さ、23は奇数ですね。
イチゴの数が奇数なら、イチゴの重さは奇数になってしまいますが、
イチゴの数が偶数なら、イチゴの重さは偶数となります。

いっぽう、マシュマロの重さ、12は偶数なので、
マシュマロの数が偶数でも奇数でも、マシュマロの重さ自体は偶数になります。

そして、イチゴとマシュマロをあわせた重さ、500は偶数です。

全体の重さ（偶数）−マシュマロの重さ（偶数）=イチゴの重さ（偶数）

となることが求められますね。つまり、イチゴの個数は偶数である必要があるのです。

一次不定方程式\( \ 23x+12y=1\ \)を解くと、
\( \ \begin{align}x=&-12k-1 \\\\y =&23k+2 \\\\ &\left( 以下\quad kは任意の整数\right) \end{align} \ \)となる.
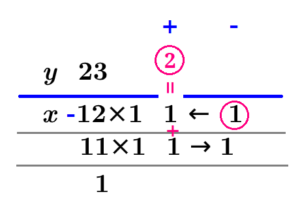それぞれの定数部分を500倍する
\( \ \begin{align}x=&-12k-500 \\\\y =&23k+1000 \end{align} \ \)
また、\( \ x \ , \ y\ \)はともに自然数であるので、

\( \ \begin{align}x=&-12k-500 \gt 0\\\\y =&23k+1000 \gt 0\end{align} \ \)

不等式を解いて

\( \ -43 \leq k \leq -41\ \)

すなわち、
\( \ \begin{align}k=&-43\quad \cdots\left( ⅰ\right) \\\\ k=&-42\quad \cdots\left( ⅱ\right) \\\\ k=&-41\quad \cdots\left( ⅲ\right) \end{align} \ \)

の3通りが考えられる。

 \( \ x=-12k-500\ \) に代入して\( \ x\ \)が偶数の自然数となる\( \ k\ \)を求める。

ⅰ）
\( \ \begin{align}x=&-12\times -43-500 \\\\ x=&16\quad \left( 条件を満たす\right) \end{align}\ \)

ⅱ）
\( \ \begin{align}x=&-12\times -42-500 \\\\ x=&4\quad \left( 条件を満たす\right) \end{align}\ \)

ⅲ）
\( \ \begin{align}x=&-12\times -41-500 \\\\ x=&-8 \quad \left( 条件を満たさない\right) \end{align}\ \)

ⅰからⅲより、条件を満たすイチゴの個数は、16個、または4個である。

また、マシュマロの個数は、それぞれ11個、34個である。

こたえ

結局、イチゴとマシュマロはどうなるのか。

こたえを求めるまでは、数学アタマでしたが、いざこたえが出るとパターン1とパターン2の違いにびっくり。
パターン1は、イチゴとマシュマロのバランスが絶妙ですね。若干イチゴが多いので、甘酸っぱさとジューシーさを楽しみつつ、マシュマロのふわふわ感に癒やされる。
お店に売ってたら、私はこっちを買うような気がします。

しかし、パターン2は、「イチゴは一人一個よ！」というパターンです。
34個のマシュマロ、どうするんだろう。。。

ディノ

ババロア（風）スイーツを作るんじゃねぇか？イチゴは、ぽちっと載せるんだよ。

Lukia

はぁ、なるほど〜。

スイーツに詳しい方、この500gパックの使いみちを思いつかれましたら、ご一報いただければと存じます。(笑)

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。