高校数学の「円と内接する四角形」に関する問題を解いてみる。（Yahoo!知恵袋より）

2020年5月25日2023年1月13日図形と計量実用数学技能検定（数学検定数検),数検準2級

読了時間: 約6分48秒

[mathjax]

問題

円に内接する四角形$ \ \mathrm{ABCD} \ $がある。対角線$ \ \mathrm{AC} \ $と$ \ \mathrm{BD} \ $は直交し、その交点を$ \ \mathrm{E} \ $とする。
$ \ \mathrm{AD}=\sqrt{13} \ , \ \mathrm{AE}=3 \ , \ \mathrm{BE}=8 \ $とする。
$ \ \mathrm{AB}=\sqrt{\color{#0004fc}{アイ}} \ $ であり、
$ \ \mathrm{CE}=\frac{\color{#0004fc}{ウエ}}{\color{#0004fc}{オ}} \ $ である。
また、円の中心を$ \ \mathrm{O} \ $とする。
$ \ \mathrm{O} \ $から直線$ \ \mathrm{BD} \ $に垂線を引き、$ \ \mathrm{BD} \ $との交点を$ \ \mathrm{F} \ $とすると
$ \ \mathrm{OF}=\frac{\color{#0004fc}{カ}}{\color{#0004fc}{キ}} \ $である。
よって円の半径は、$ \ \frac{\sqrt{\color{#0004fc}{クケコ}}}{\color{#0004fc}{サ}} \ $ である。
また、点$ \ \mathrm{A} \ $を通りこの円に接する直線と、直線$ \ \mathrm{BD} \ $との交点を$ \ \mathrm{G} \ $とすると
$ \ \mathrm{DG}=\frac{\color{#0004fc}{シス}}{\color{#0004fc}{セ}} \ $である。

解法

ア〜オを解く。

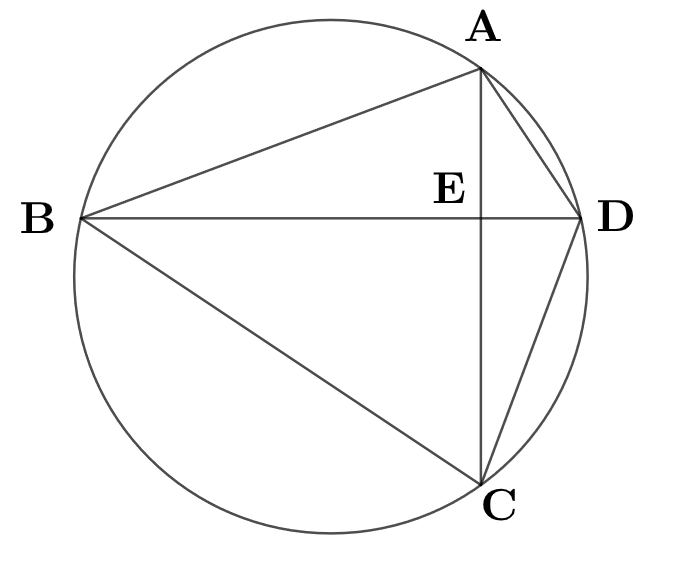
$ \ \triangle \mathrm{ABE} \ $において三平方の定理より
$ \ \begin{align}\mathrm{AB}^2=&\mathrm{AE}^2+\mathrm{BE}^2 \\\\ =&9+64 \\\\ =&73 \end{align} \ $
$ \ \mathrm{AB} \gt 0\ $より$ \ \mathrm{AB}=\sqrt{73} \ $

また同様に
$ \ \triangle \mathrm{AED} \ $において三平方の定理より
$ \ \mathrm{ED}=2 \ $

$ \ \triangle \mathrm{AEB} \ $と$ \ \triangle \mathrm{DEC} \ $ において
弧$ \ \mathrm{AB} \ $に対する円周角(inscribed angles)より
$ \ \angle \mathrm{ABE}=\angle \mathrm{DCE} \ $

同様に
弧$ \ \mathrm{BC} \ $に対する円周角(inscribed angles)より
$ \ \angle \mathrm{EAB}=\angle \mathrm{EDC} \ $

二つの角の大きさがそれぞれ等しいので、
$ \ \triangle \mathrm{AEB} \sim \triangle \mathrm{DEC} \ $である。
相似比は$ \ \triangle \mathrm{AEB} ： \triangle \mathrm{DEC} =3：2\ $より、

$ \ \mathrm{CE}=\frac{16}{3} \ $

カ〜サを解く。

Lukia

問題では、カ・キを先に答えるような誘導となっていますが、
私の能力ではその誘導には従えなかったので、
四角形ABCDの外接円の半径を先に求めてから「カ・キ」を求めようと思います。

$ \ \triangle \mathrm{ABD} \ $の面積を$ \ \mathrm{S} \ $、四角形ABCDの外接円の半径を$ \ \mathrm{R} \ $とする。
$ \ \begin{align}\mathrm{S}=&\frac{1}{2}\mathrm{AB}\times \mathrm{AD}\times \sin \angle \mathrm{BAD}=\frac{1}{2}\mathrm{BD}\times \mathrm{AE} \\\\ =&\frac{1}{2}\times \sqrt{73}\times \sqrt{13}\times \sin \angle \mathrm{BAD}=\frac{1}{2}\times 10\times 3\end{align} \ $
整理すると
$ \ \sin \angle \mathrm{BAD}=\frac{30}{\sqrt{73}\times \sqrt{13}} \ $

また正弦定理(Sine Formula)より
$ \ \begin{align}\sin \angle \mathrm{BAD}=&\frac{\mathrm{BD}}{2\mathrm{R}} \\\\ =&\frac{10}{2\mathrm{R}} \end{align} \ $

以上より
$ \ \begin{align}\frac{10}{2\mathrm{R}} =&\frac{30}{\sqrt{73}\times \sqrt{13}} \\\\ \mathrm{R}=&\frac{\sqrt{949}}{6} \end{align} \ $

知っておくと便利な公式

$$\Large 4\mathrm{RS}=abc$$

円に内接する三角形の3辺の積は、外接円の半径と三角形の面積の積を4倍したものに等しい。

Lukia

今回の問題の場合、$ \ \triangle \mathrm{ABD} \ $に関して情報が豊富なので、
この公式を知っていると、外接円の半径が簡単に導けます。
以下に三角形ABCとその外接円を示し、公式を導出してみます。

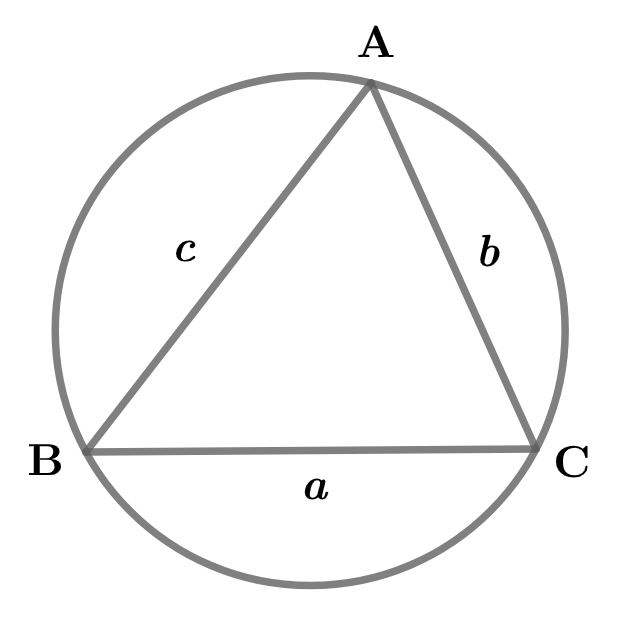
三角形の面積$ \ \mathrm{S} \ $は、

$ \ \mathrm{S}=\frac{1}{2}bc\sin \mathrm{A} $

また、三角形の外接円の半径を$ \ \mathrm{R} \ $とする。
正弦定理より

$ \ \sin \mathrm{A}=\frac{a}{2\mathrm{R}} \ $

$ \ \begin{align}\mathrm{S}=&\frac{1}{2}bc\sin \mathrm{A} \\\\ =&\frac{1}{2}bc \\\\ =&\frac{a}{2\mathrm{R}}\\\\ \\\\ 4\mathrm{RS}=&abc \end{align} \ $

Lukia

今回の問題は、三角形BADの3辺の長さもわかっているし、高さもわかっているので、
この公式を知っていれば、一気に計算すればよいですね。
また、知らない場合でも、別に$ \ \sin \angle \mathrm{BAD} \ $を丁寧に求める必要はなく、途中までで置いといて、面積を求める式に当てはめていけば、やっていることは、上記の公式と同じことです。

円の中心$ \ \mathrm{O} \ $から弦$ \ \mathrm{BD} \ $へおろした線分$ \ \mathrm{OF} \ $は
弦$ \ \mathrm{BD} \ $の垂直二等分線である。
ゆえに、$ \ \triangle \mathrm{BFO} \ $は、$ \ \angle \mathrm{OFB}=90^{\circ} \ $の直角三角形である。

$ \ \triangle \mathrm{BFO} \ $において
$ \ \begin{align}\mathrm{OF}^2=&\mathrm{BO}^2-\mathrm{BF}^2 \\\\ =&\frac{949}{36}-25\times \frac{36}{36} \\\\ =&\frac{49}{36} \end{align} \ $
$ \ \mathrm{OF} \gt 0\ $より
$ \ \mathrm{OF}=\frac{7}{6} \ $

シ〜セを解く。

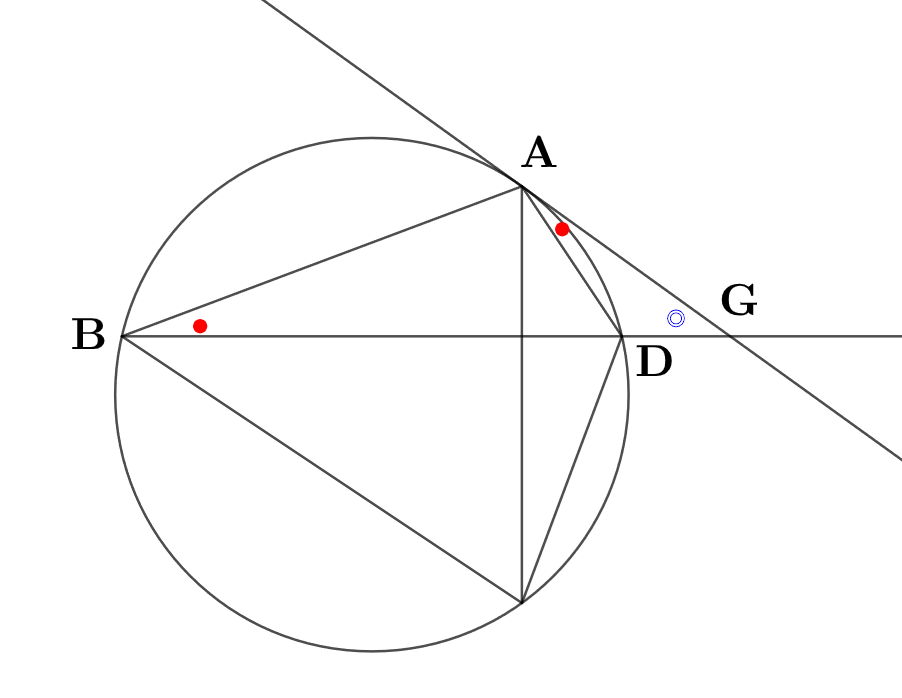
$ \ \triangle \mathrm{ADG} \ $と$ \ \triangle \mathrm{BAG} \ $において
$ \ \angle \mathrm{AGD}=\angle \mathrm{BGA} \ $・・・◎
また接弦定理(alternate segment theorem)より
$ \ \angle \mathrm{GAD}=\angle \mathrm{GBA} \ $・・・●
二つの角の大きさがそれぞれ等しいので

$ \\triangle \mathrm{ADG} \sim \triangle \mathrm{BAG} \ $である

ここで辺$ \ \mathrm{DG} \ $の長さを$ \ x\ $とすると、
辺$ \ \mathrm{BG} \ $の長さは$ \ 10+x\ $と表せる。

方べきの定理(Power of a point Theorem)より
$ \ \begin{align}\mathrm{AG}^2=&\mathrm{BG}\cdot \mathrm{DG} \\\\ \left( \frac{\sqrt{73}x}{\sqrt{13}}\right)^2=&\left( 10+x\right)\cdot x\\\\ \frac{73x^2}{13}=&\left( 10x+x^2\right)\\\\ 73x^2=&13x^2+130x\\\\ 60x^2=&130x\\\\ &x \gt 0\quad より\\\\ 6x=&13\\\\ \\\\ x=&\frac{13}{6} \end{align} \ $

ゆえに$ \ \mathrm{DG}= \frac{13}{6} \ $