高校数学の「三角比と内接円・外接円」に関する問題を解いてみる。（Yahoo!知恵袋より）

おかれているのは「辺の長さの比」と考える。

Lukia

よく見ると、辺の長さは書かれていませんね。
\( \ \frac{\sin \mathrm{A}}{6}=\frac{\sin \mathrm{B}}{5}=\frac{\sin \mathrm{A}}{4} \ \)
の分母が角に対する辺の長さなんじゃない？と考える人もいるかもしれませんが、（2）で内接円の半径の長さが具体的に設定されているので、これと矛盾するおそれがあります。中学校の数学で三角形の相似の条件を習ったと思いますが、2つの角の大きさがそれぞれ等しければ、相似（拡大・縮小）の関係にあるといえましたね。
ここでは、いったん定数\( \ k \ \)を設定してやって、それぞれの辺の長さの比が\( \ \mathrm{BC}:\mathrm{CA}:\mathrm{AB}=6:5:4 \ \)である三角形として考えていきましょう。

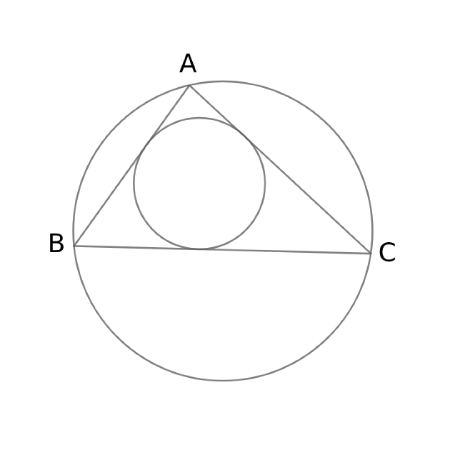
$$\begin{align}\triangle \mathrm{ABC}に&おいて、\\\\ 三辺の&比がそれぞれ \\\\ \mathrm{BC}:\mathrm{CA}:\mathrm{AB}=6:5:4 \ であるとする。\\\\ 三辺の&長さは、\\\\ それぞれ\quad \ & \mathrm{BC}=6k \ , \ \mathrm{CA}=5k \ , \ \mathrm{AB}=4k\\\\ \quad \ & \left( k \ は正の実数\right) \quad と表せる。\end{align}$$

(1)を求める。

余弦定理より
$$\begin{align}\cos \mathrm{A}=&\frac{\mathrm{AC}^2+\mathrm{AB}^2-\mathrm{BC}^2}{2\mathrm{AC}\cdot \mathrm{AB}} \\\\ =&\frac{25k^2+16k^2-36k^2}{2\cdot 5k\cdot 4k} \\\\ =&\frac{1}{8} \end{align}$$

また、
$$\begin{align}\sin \mathrm{A}=&\sqrt{1-\cos^{2} \mathrm{A}}\quad \left( 0 \lt \mathrm{A} \lt \pi\right) \\\\ =&\frac{3\sqrt{7}}{8} \end{align}$$

Lukia

三角形の内角の和は\( \ 180^{\circ} \ \) です。
\( \ \angle \mathrm{A} \ \)が鋭角にしろ鈍角にしろ、サインの値は正のままですよね。
\( \ \left( 0 \lt \mathrm{A} \lt \pi\right) \ \)は、
「私は、いきなりルートをかぶせたんじゃないですよ。内角の大きさがどうであれ、サインの値は正となるということがわかってるから、こうしたんですよ。」というアピールになります。
たしかに、書いてないと、乱暴な気がしますし、たまたま合ってた感が醸し出されてしまいますね。

(2)を求める。

$$\triangle \mathrm{ABC}の面積を \ \mathrm{S} \ とする.$$
$$\begin{align}\mathrm{S}=&\frac{1}{2}\mathrm{AC}\cdot \mathrm{AB}\sin \mathrm{A}=\frac{15\sqrt{7}}{4}k^2 \end{align}$$

$$\begin{align}また,&\triangle \mathrm{ABC}の内接円の半径を \ r \ とし, \\\\ s=&\frac{\mathrm{BC}+\mathrm{CA}+\mathrm{AB}}{2} \ とする.\\\\ \mathrm{S}=&rs=1\cdot \frac{\left( 6+5+4\right)k}{2}=\frac{15}{2}k\\\\ \frac{15\sqrt{7}}{4}k^2=&\frac{15}{2}k\\\\ k=&\frac{2\sqrt{7}}{7}\\\\ \mathrm{AB}=&4k=4\cdot\frac{2\sqrt{7}}{7}= \frac{8\sqrt{7}}{7}\\\\ \mathrm{S}=&rs=1\cdot \frac{15}{2}\cdot \frac{2\sqrt{7}}{7}= \frac{15\sqrt{7}}{7} \end{align}$$

外接円の半径の求め方2通り

Lukia

外接円の半径の求め方を2通り表しておきます。
自分に適した方を用いるようにしましょう。

正弦定理を用いる

$$\triangle \mathrm{ABC}の外接円の半径を \ \mathrm{R} \ とする.$$
正弦定理より
$$\begin{align}2\mathrm{R}=&\frac{\mathrm{BC}}{\sin \mathrm{A}} \\\\ =&6\cdot\frac{2\sqrt{7}}{7}\cdot \frac{8}{3\sqrt{7}} \\\\ =&\frac{32}{7}\\\\ \mathrm{R}=&\frac{16}{7} \end{align}$$

三角形の面積と三辺の長さを用いる

$$\begin{align}4\mathrm{RS}=&\mathrm{BC}\cdot \mathrm{CA}\cdot \mathrm{AB} \\\\ 4\mathrm{R}\cdot rs=&4\cdot 5\cdot 6k^3 \\\\ 4\cdot 1\cdot \frac{15}{2}k\mathrm{R}=&4\cdot 5\cdot 6k^3\\\\ \mathrm{R}=&4k^2\\\\ \mathrm{R}=&\frac{16}{7} \end{align}$$

Lukia

今回の問題の場合、正の実数\( \ k \ \)が平方根を含んでるわ、分数の形になるわで大変な値をとっていますから、すんなり正弦定理から求めたほうが楽そうですね。
しかし、数値によっては、正弦定理を経ずに、面積と三辺の長さから外接円の半径を求めたほうが楽なこともあります。
こればっかりはケースバイケースだろうと思いますので、似たような問題をいくつかやって、自分なりのルールを作っていくとよいと思います。

こたえ

$$\begin{align}\cos \mathrm{A}=&\frac{1}{8} \\\\ \sin \mathrm{A}=&\frac{3\sqrt{7}}{8} \\\\ \mathrm{AB}=&\frac{8\sqrt{7}}{7} \\\\ \triangle \mathrm{ABC}の面積:&\frac{15\sqrt{7}}{7}\\\\ \triangle \mathrm{ABC}の外接円の半径:&\frac{16}{7} \end{align}$$