高校数学の「ユークリッドの互除法」に関する問題を解いてみる。(Yahoo!知恵袋より)

[mathjax]
これらのうち、それぞれ2種類あるいは3種類すべてを混ぜ合わせて,
濃度が6.4% の食塩水を100g 作るとき,
1%の食塩水は,何g 以上 何g 以下まで使用できるか。
また,10% の食塩水は,何g 以上 何g 以下まで使用できるか。
なんとゴルフ練習場で解いた問題。
この問題、Yahoo!知恵袋の高校数学カテゴリに投稿されていたものの、
中学数学なのではないか?と思っていました。
実際、中学数学のペルソナ、ももちゃんを登場させて、かなり長編の記事を書いていたのですが、
最後の最後で行き詰ってしまいました。
一度は、公開することそのものをあきらめ、ごみ箱に放り込んだのですが、どうにもあきらめがつかない。
当初考えていた解法には、なんと6つもの場合分けがあり、

Lukia
中学数学で場合分け自体をあまりやらないだろうから、やっぱりカテ違いではなくて、高校数学内容なんだよね・・・。
こんなに手間取る問題じゃないはずなんだよね・・・。
こんなにもまどろっこしい問題であるわけがないので、アプローチの仕方が間違っているんだろうな。と思い、別の方法を考えることにしました。
とあるアイディアが浮かんだところで、

夫
と言うので、私も、暇つぶしの道具を持って、くっついていくことにしました。

Lukia
夫がぶんぶんゴルフクラブを振り回すのをぼんやり視界に入れながら、私はこの問題を解いていきました。
食塩水が出てくるので、中学数学の文章題かと思っていましたが、しっかり高校数学の問題でした。(^◇^;)
ユークリッドの互除法に持ち込む。
| 1% | 10% | 5% | 6.4% | |
| 百分率 | $$\frac{1}{100}$$ | $$\frac{10}{100}$$ | $$\frac{5}{100}$$ | $$\frac{6.4}{100}$$ |
| 食塩水の重さ | $$x$$ | $$y$$ | $$z$$ | $$100$$ |
| 食塩の重さ | $$\frac{1}{100}\times x$$ | $$\frac{10}{100}\times y$$ | $$\frac{5}{100}\times z$$ | $$\frac{6.4}{100}\times 100$$ |
$$\begin{align}1% \ の食塩水&の重さを\quad x \ \mathrm{g} \ とし, \\\\ \left( 0 \leq x \lt 100\right) \ 10% \ の食塩水&の重さを\quad y \ \mathrm{g} \ とし, \\\\ \left( 0 \leq y \lt 100\right) \ 5% \ の食塩水&の重さを\quad z \ \mathrm{g} \ とする. \\\\ \left( 0 \leq z \lt 100\right) \end{align}$$

Lukia
100以下(100も含む)とすると、1種類の食塩水で、6.4%の濃度を作ることになるからです。
1%はどうあがいても、6.4%にはなりません。
ゆえに、100以下とするのはおかしいですよね。
$$\begin{align}x+y+z=&100\quad より, \\\\\ z=&100-x-y\quad と表せる.\end{align}$$
$$\begin{align}\frac{1}{100}\times x+\frac{10}{100}\times y+\frac{5}{100}\times \left( 100-x-y\right)&=\frac{6.4}{100}\times 100 \\\\ x+10y+500-5x-5y&=640 \\\\ -4x+5y&=140 \end{align}$$
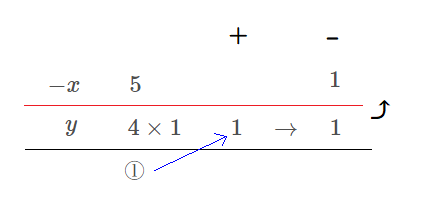
ユークリッドの互除法より
$$\begin{align}-x=&5k-140\quad \cdots \ ① \\\\ y=&-4k+140\quad \cdots \ ② \\\\ &\left( k \ は実数\right) \end{align}$$
と表せる。
$$\begin{align}①より& \\\\ x=&-5k+140 \\\\ 0 \leq &-5k+140 \lt 100\\\\ -140 \leq &-5k \lt -40\\\\ 8 \lt &k \leq 28\end{align}$$
$$\begin{align}②より& \\\\ y=&-4k+140 \\\\ 0 \leq &-4k+140 \lt 100\\\\ -140 \leq &-4k \lt -40\\\\ 10 \lt &k \leq 35\end{align}$$
$$\begin{align}以上より&\quad 実数 \ k \ の範囲は, \ &\quad 10 \lt k \leq 28\quad である.\end{align}$$
$$\begin{align}ゆえに&x\quad の範囲は, \\\\ &-28\color{#0004fc}{\times 5+140} \leq -k\color{#0004fc}{\times 5+140} \lt -10\color{#0004fc}{\times 5+140} \\\\ &0 \leq x \lt 90\ \\\\ &y\quad の範囲は,\\\\ &-28\color{#0004fc}{\times 4+140} \leq -k\color{#0004fc}{\times 4+140} \lt -10\color{#0004fc}{\times 4+140}\\\\ &28 \leq y \lt 100 \end{align}$$
でも、まだしっくりこない。
いったんは、(答えが出た~♪)と思ったものの、どうもしっくりきません。
問題文をよく読むと、1%食塩水も、10%食塩水も、「何g以上何g以下利用できる」となっています。
私の答えでは、下限はわかっているものの、上限がはっきりしていないので、これではまだ答えの途中のような気がしていました。
そうこうしていると、クラブをぶんぶん振り回して疲れた夫が、

夫
と言い出したので、いったん中断しました。
昼食や買い物などを済ませ、あらためて問題を見なおしてみると、
ここまでの解法は、用いる食塩水の濃度が2種類でもいいけど、最大3種類使ったときのことを考えて式を立てたものとなっています。
使う食塩水を2種類と限定したときのことは、まだ考えていません。
上限がはっきりしないのは、この2種類を使った場合を考えていないからではないかと思い、ここを考えてみることにしました。
2種類の食塩水を使う場合。
2種類の食塩水を用いて、6.4%の食塩水を100g作るには,
ⅰ)1%食塩水と10%食塩水を用いる場合
ⅱ)10%食塩水と5%食塩水を用いる場合
の2通りが考えられる。

Lukia
本来は3通り考えるべきなのですが、上記の理由で2通りとなっています。
ⅰ)1%食塩水と10%食塩水を用いる場合
$$\begin{align}1%\quad &の食塩水の重さを\quad x \ \mathrm{g} \ とする. \\\\ x+10\left( 100-x\right)=&640\quad を解いて, \\\\ x=40& \end{align}$$
ゆえに1%の食塩水は 40g , 10%の食塩水は 60g 用いられる.
ⅱ)10%食塩水と5%食塩水を用いる場合
$$\begin{align}10%\quad &の食塩水の重さを\quad y \ \mathrm{g} \ とする. \\\\ 10y+5\left( 100-y\right)=&640\quad を解いて, \\\\ y=28& \end{align}$$
ゆえに10%の食塩水は 28g , 5%の食塩水は 72g 用いられる.

Lukia
$$\begin{align}以上より& \ &0 \leq x\color{#0004fc}{ \leq 40} \ \ &28 \leq y\color{#0004fc}{ \leq 60} \end{align}$$
ゆえに、1%の食塩水は, 0g以上40g以下 用いることができる.
また、 10%の食塩水は, 28g以上60g以下 用いることができる.

Lukia
そこから3種類使った場合というのを考えるほうが、思いつきやすいと思います。
ですから、解答作成の順番が前後しているほうが、自然かもしれませんね。
こたえ
1%の食塩水は, 0g以上40g以下 用いることができる.
10%の食塩水は, 28g以上60g以下 用いることができる.
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません