高校数学の「命題の真偽(絶対値を含んだ不等式)」に関する問題を解いてみる。【Yahoo!知恵袋より】

読了時間: 約1分4秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「命題の真偽(絶対値を含んだ不等式)」に関する問題を解いてみました。
問題
\( \ 2\vert x-2 \vert-x \gt 0 \ \) ならば \( \ x \gt 4 \ \) である
この真偽を確かめよ。
この真偽を確かめよ。
解法

命題の真偽は、
\( \ 2\vert x-2 \vert-x \gt 0 \ \) で示される\( \ x \ \)の範囲が、もれなく \( \ x \gt 4 \ \) に含まれていれば「真」、
反対に、たった一例でも例外があれば、「偽」となります。
\( \ 2\vert x-2 \vert-x \gt 0 \ \) で示される\( \ x \ \)の範囲が、もれなく \( \ x \gt 4 \ \) に含まれていれば「真」、
反対に、たった一例でも例外があれば、「偽」となります。
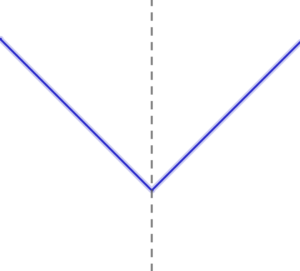 |
|
| \( \ x \lt 2 \ \) のとき | \( \ 2 \leqq x \ \) のとき |
| \( \ 2\left( -x+2\right)-x \gt 0 \ \) \( \ -2x+4-x \gt 0 \ \) \( \ -3x \gt 4 \ \) \( \ x \lt -\displaystyle\frac{4}{3} \ \) |
\( \ 2\left( x-2\right)-x \gt 0 \ \) \( \ 2x-4-x \gt 0 \ \) \( \ x \gt 4 \ \) |
\( \ x \lt -\displaystyle\frac{4}{3} \ \) または \( \ 4 \lt x \ \)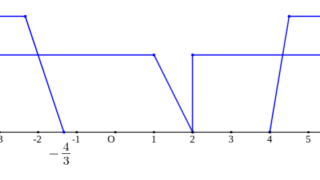 |
|
こたえ
「偽」[subscribe2]









ディスカッション
コメント一覧
まだ、コメントがありません