刺し子柄の八ツ手麻の葉を数式で表し、グラフに描いてみた。

[mathjax]
趣味と実益を兼ねる「刺し子ふきん」
ここ数年、趣味と実益を兼ねて、「刺し子ふきん」の作成にいそしんでおります。
一番最初は、運針ができるようになりたくて、さらしにぶしぶし波縫いをしただけのふきんでしたが、
不揃いな針目と、使ううちにやわらかなくたっとした風合いに変化していくところが気に入って、よく使っておりました。
結局、気がつけば、4年ぐらい使っていましたね。
結局、運針は上手にならないままでしたが、ひたすら波縫いをする。というルーティンワークが気に入り、
今度は、模様を縫ってみることにしました。

Lukia
2018年秋ごろ?は、図書館で本を借りたり、Googleの画像検索をしてみたりして、やってみたい図柄を探し、あれこれ縫ったように思います。
しかし、2018年末に転居があったり、2019年は、10年ぶりの社会復帰を果たして忙しくなり、思ったほど刺し子ができませんでした。
無性に刺し子がしたいのよ。(涙)
勉強やパソコン作業をしすぎて頭がぼーっとすると、ルーティンワークがしたくなります。
私の場合、それが「いりこの頭とワタ取り」だったり、

「編み物(輪針でアクリルたわしを編みます)」だったりするのですが、

今回は、無性に刺し子がしたくなっておりました。

Lukia
麻の葉柄が縫いたい!
六角形縫いたい!
パソコン作業で頭がぽ〜っとしている中ひらめいた私は、仕事帰りのバスの中で早速刺し子柄の画像検索をするのでした。
麻の葉柄の変異型、「八ツ手麻の葉」にビビッ!とくる。
麻の葉柄は以前も縫ったことがあり、好きな柄なのですが、Googleで画像検索していたら、麻の葉柄の変異型?を見つけ、
これッ!と思ってしまいました。
八ツ手麻の葉です。
正方形とひし形が組み合わさってできているので、シンプルで、縫いやすく、それでいて見栄えもよい。
検索した画像では、一枚のふきんにいくつもの八ツ手麻の葉があしらわれていましたが、
短時間ちょっと刺し子を楽しみたい私は、一枚のふきんにど〜んと大きな八ツ手麻の葉をあしらうことにしました。
そしてできたのがこれ。

直線縫いをしただけなのに、なんて見栄えのする柄なんでしょう。
すっかり好きになってしまいました。
また、2〜3時間もあれば十分縫えますから、直線縫いに飽きそうな頃に仕上がるのも魅力です。
この一枚でやめるつもりでしたが、刺し子に対する欲求が強まり、
もう一枚、同じ柄を縫いました。


Lukia
と思ってしまいました。(笑)
黒いさらしは、もう何ヶ月も前から買ってあったものです。
切り分けるサイズも決めているのだから、測って切ればいいだけなのに、なかなかその気になれずにいました。
しかし、この八ツ手麻の葉のおかげで、黒いさらしも切り分けることができました。

Lukia
黒地にピンクの糸が走るようすは、すごくかわいいです。
そろそろ梅の時期ですし、黒地にピンクと黄緑の糸で、暗闇に浮かぶ紅梅を描いたらきれいだろうな〜。と新たな創作意欲にかりたてられたり、
黒いさらしは、明るくて淡い色(黄色や黄緑など)を引き立てそうだなと思ったので、
レモンイエローの刺し子糸を探して、レモンの柄などを刺してみたいなと思ったりしています。
ただ、白いさらしなら、フリクションペンで下描きができるのですが、黒いさらしはそうはいきません。
手持ちのチャコを使ってみましたが、先が鈍っているので、細かく正確な線を引けないので、
新たにチャコペーパーなどを買い、カーボン紙の要領で図柄を写してみようかなと思っています。
八ツ手麻の葉を数式で表してみる
下描きをしている最中も、縫っている最中も、

Lukia
と思っていたので、考えてみました。
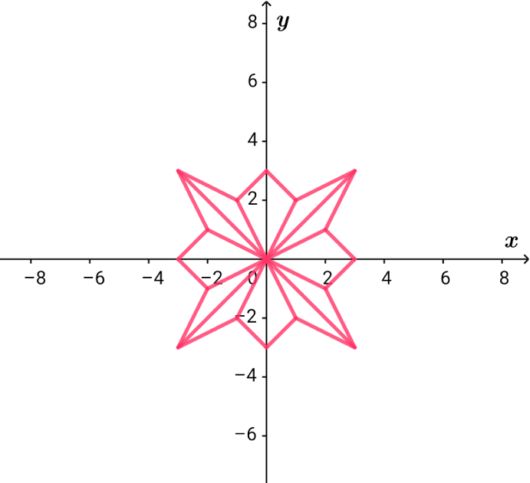
$$\begin{align} y=&-x+3 \ \left( 0 \leq x \leq 1 \ かつ \ 2 \leq x \leq 3\right) \\\\ y=&x+3 \ \left( -3 \leq x \leq -2 \ かつ \ -1 \leq x \leq 0\right) \\\\ y=&-x-3 \ \left( -3 \leq x \leq -2 \ かつ \ -1 \leq x \leq 0\right) \\\\ y=&x-3 \ \left( 0 \leq x \leq 1 \ かつ \ 2 \leq x \leq 3\right) \end{align}$$

Lukia
$$\begin{align}y=&x \ \left( -3 \leq x \leq 3\right) \\\\ y=&-x \ \left( -3 \leq x \leq 3\right) \\\\
\end{align}$$

Lukia
$$\begin{align}y=&2x \ \left( -1 \leq x \leq 1\right) \\\\ y=&-2x \ \left( -1 \leq x \leq 1\right)\\\\ y=&2\left( x-3\right)+3 \ \left( 2 \leq x \leq 3\right) \\\\ y=&2\left( x+3\right)-3 \ \left( -3 \leq x \leq -2\right) \\\\ y=&-2\left( x-3\right)-3 \ \left( 2 \leq x \leq 3\right)\\\\ y=&-2\left( x+3\right)+3 \ \left( -3 \leq x \leq -2\right) \end{align}$$

Lukia
$$\begin{align}y=&\frac{1}{2}\left( x-3\right)+3 \ \left( 2 \leq x \leq 3\right) \\\\ y=&\frac{1}{2}\left( x+3\right)-3 \ \left( -3 \leq x \leq -2\right) \\\\ y=&- \frac{1}{2}\left( x-3\right)-3 \ \left( 2 \leq x \leq 3\right)\\\\ y=&-\frac{1}{2}\left( x+3\right)+3 \ \left( -3 \leq x \leq -2\right) \end{align}$$

Lukia
なんと12もの式が必要となるわけですね。
こりゃ〜なんぼ正確無比でも、グラフ描画ソフトに頼るよりは、ものさしとペンで下描きするほうがよさそうです。(笑)
[subscribe2]









ディスカッション
コメント一覧
まだ、コメントがありません