平面ベクトル三角形の内分比を統一する（その2）【たすきがけで比を統一せよ!!】

2023年1月7日ベクトル実用数学技能検定（数学検定 数検),数検2級,数検準1級

内分の比を「統一」する。

Lukia

適当な三角形を描いて、内分比を書き込んでいきます。
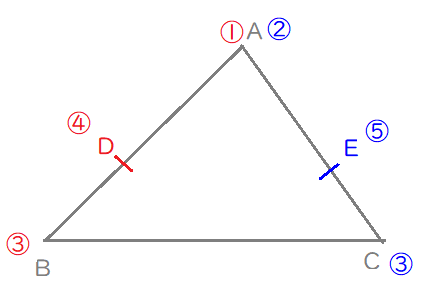
辺\(\mathrm{AB}\)を\(3：1\)に内分するに点\(\mathrm{D}\)を打ち、たすき掛けするように、反対側の頂点に内分比を書き込みます。
私は、比と辺の長さが区別しやすいよう、比の数値を〇や□で囲みます。
辺\(\mathrm{AC}\)についても同様に内分比を書き込みます。

Lukia

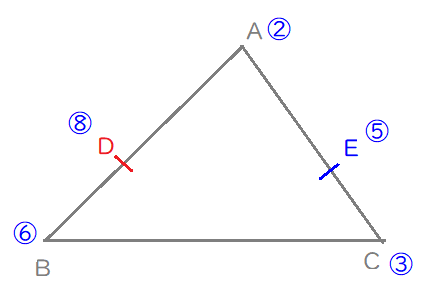
ここで、赤の内分比を2倍すれば、青の内分比に統一できそうなので、
赤の内分比を書き換えます。

Lukia

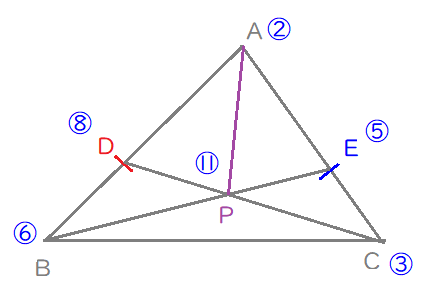
辺\(\mathrm{BE}\)と辺\(\mathrm{CD}\)を結び、交点\(\mathrm{P}\)を定めます。
交点\(\mathrm{P}\)は、辺\(\mathrm{BE}\)と辺\(\mathrm{CD}\)それぞれの内分点であるとわかりますね。
内分点自体の比は、両端の比の和で求められますから、\(11\)です。

Lukia

\(\overrightarrow{\mathrm{AP}}=s\overrightarrow{\mathrm{AB}}+t\overrightarrow{\mathrm{AC}}\)
\(\left( ただし, \ s \ , \ t \ は任意の実数\right)\)で表せ。とありましたから、
点\(\mathrm{A}\)以外の点に書いてある比をまずは、ベクトルの前に書いてやりましょう。

$$\begin{align}11\overrightarrow{\mathrm{AP}}=&6\overrightarrow{\mathrm{AB}}+3\overrightarrow{\mathrm{AC}} \\\\ \\\\ \overrightarrow{\mathrm{AP}}=&\displaystyle\frac{3}{11}\left( 2\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}\right) \end{align}$$

こたえ

$$\overrightarrow{\mathrm{AP}}=\displaystyle\frac{3}{11}\left( 2\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}\right)$$

平面ベクトル三角形の内分点 記事一覧【たすきがけで比を統一せよ!!】

平面ベクトルの習い始めによく演習する「三角形の内分点」に関する問題を集めました。一見難しそうな外 ...

 https://makelemonadejp.com/plane-vector-internal-division-of...

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。