複数のヒントから3つの数字を特定する

インスタグラムで面白い問題を見つけました。
解いて答えをコメントで送ると、正誤の判定をしてくれます。
 ヒントを和訳し、解いてみます。
ヒントを和訳し、解いてみます。

条件4からしぼりこむ
条件4の「いずれも正しくない」より、
\( \ 7 \ \)と\( \ 3 \ \)と\( \ 8 \ \)は、この鍵の数字には含まれていないことになります。
条件1から条件5までの3つの数字にある\( \ 7 \ \)と\( \ 3 \ \)と\( \ 8 \ \)を消します。

条件5から1つ数字がわかる
条件4で3つの数字を消したことにより、条件5の3つの数字のうち、\( \ 0 \ \)の1つだけが消されずに残りました。
そして、条件5は、「1つの数字が正しいが、間違った場所にある」ということですので、
\( \ 0 \ \)が右端にあってはならないことになります。
ゆえに、3桁の数字は、「○ \( \ 0 \ \) ○」か、「 \( \ 0 \ \) ○ ○」であることになります。

条件3より場合分けで考える
条件3は、「2つの数字が正しいが、(それぞれ)間違った場所にある」です。
まず、条件4と5により、 \( \ 0 \ \)は正しい数字だとわかりました。
そして、条件3の数字にも \( \ 0 \ \)が含まれています。
しかし、もう1つ含まれた正しい数字が \( \ 2 \ \)と \( \ 6 \ \)のどちらかはわかりません。
以降、場合分けをしてどちらが正しい数字なのかを特定していきます。
その前に、 \( \ 0 \ \)の位置は正しくない。とのことでした。
よって、3桁の数字は、「 \( \ 0 \ \) ○ ○」であることになります。
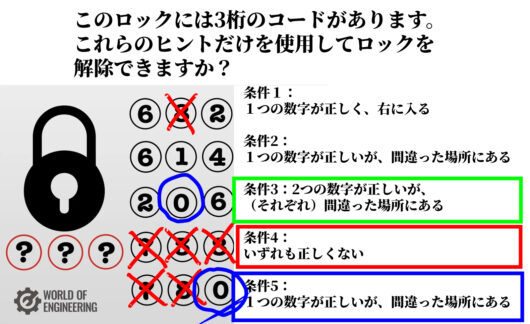
仮定1:2が正しい数字であるとき
仮に、 \( \ 0 \ \)と \( \ 2 \ \)が正しい数字だとします。
ひとまず、3桁の数字は、「 \( \ 0 \ \) \( \ 2 \ \) ○」または、「 \( \ 0 \ \) ○\( \ 2 \ \) 」であることになります。
また、逆に\( \ 6 \ \)は誤った数字ということになりますね。
すると条件1が「1つの数字が正しく、右に入る」とあることより、
3桁の数字は、「 \( \ 0 \ \) ○\( \ 2 \ \) 」であるとわかりました。
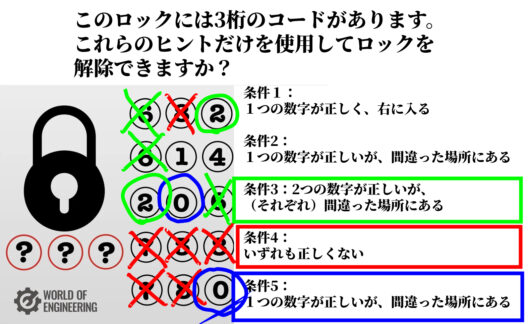 さらに条件2で真ん中の数字を特定します。
さらに条件2で真ん中の数字を特定します。
3桁の数字は、「 \( \ 0 \ \) \( \ 1 \ \) \( \ 2 \ \) 」か「 \( \ 0 \ \) \( \ 4 \ \) \( \ 2 \ \) 」であると考えられますが、
条件2が「1つの数字が正しいが、間違った場所にある」ということより、「 \( \ 0 \ \) \( \ 1 \ \) \( \ 2 \ \) 」が正しくないことがわかります。もし\( \ 1 \ \)が正しい数字だとすると、「間違った場所にある」という条件にそぐわないからです。(正しい数字が正しい場所にあることになってしまいますね)
よって、求める3桁の数字は、「 \( \ 0 \ \) \( \ 4 \ \) \( \ 2 \ \) 」となります。

仮定2:6が正しい数字であるとき
仮定1で求める3桁の数字が特定できましたが、本当に正しいのか、別解はないのかを確かめる必要があります。
仮に、\( \ 0 \ \)と\( \ 6 \ \)が正しい数字だとします。
ひとまず、3桁の数字は、「 \( \ 0 \ 6 \ \) ○」または、「 \( \ 0 \ \)○\( \ 6 \ \)」であることになります。
また、逆に\( \ 2 \ \)は誤った数字ということになりますね。
すると条件1が「1つの数字が正しく、右に入る」とあることより、
3桁の数字は、「 \( \ 0 \ \) ○\( \ 6 \ \) 」であるとわかりました。
条件2でも、\( \ 6 \ \) が「1つの数字が正しいが、間違った場所にある」という条件は満たしているといえますね。
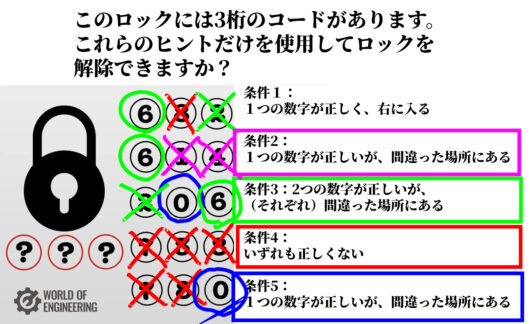
しかし、条件2が\( \ 6 \ \) に使われてしまったことで、真ん中の数字がわからなくなってしまいます。
条件2により\( \ 1 \ \)と\( \ 4 \ \) はどちらも正しくない数字ですから、入れてはいけないことになります。
 となると、\( \ 5 \ \) か\( \ 9 \ \)の可能性が出てきますが、「これらのヒントだけを使用して」とあるのに、
となると、\( \ 5 \ \) か\( \ 9 \ \)の可能性が出てきますが、「これらのヒントだけを使用して」とあるのに、
まだ別のヒントが必要になるようでは、そもそもの条件を満たしていないことになりますね。
よって、 「\( \ 0 \ \)と\( \ 6 \ \)が正しい数字」だという仮定は成立しないことになります。
ゆえに、正しい3桁の数字は、仮定1で求めた「 \( \ 0 \ \) \( \ 4 \ \) \( \ 2 \ \) 」となります。
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません