勝敗は順番次第!?【粗忽な大人、高校入試問題を解く〜それ、誤答です！〜】

2022年4月19日2023年1月9日中学数学

読了時間: 約3分29秒

広島県公立高校入試の2022年、2021年、2020年の数学の問題を解いてみました。
深い読解能力と素早い処理能力が必要とされる問題になっているな。と感じました。
3ヶ年分の問題のうち、私がおっちょこちょいなことをしたり、ツメが甘くて間違えた問題について解き直してみようと思います。

Lukia

確率は決して簡単ではありませんが、表を書いて、ていねいに数え上げる力があれば、確実に点数が取れる分野ではあります。

問題

太郎さんと次郎さんは、次の【ゲーム】において、先にカードを取り出す人と、後からカードを取り出す人とでは、どちらが勝ちやすいかを調べることにしました。

【ゲーム】

上の図のように、1,2,3,4の数字が1つずつ書かれた4枚のカードが入った袋があります。
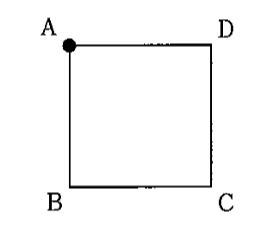
下の図のように、正方形ABCDの頂点Aにコマを置きます。このコマを、太郎さんと次郎さんの2人が、下の<ルール>にしたがって、正方形ABCDの頂点から頂点へ移動させ、勝敗を決めます。

<ルール>

1. 先に、太郎さんが袋の中のカードをよく混ぜ、そこから1枚取り出し、カードに書かれた数字の数だけ、正方形の頂点から反時計まわりにコマを移動させる。
2. 太郎さんは、取り出したカードを袋に戻し、次郎さんに交代する。
3. 次に、次郎さんが袋の中のカードをよく混ぜ、そこから1枚取り出し、1.で移動させたコマが置いてある頂点から、カードに書かれた数字の数だけ、正方形の頂点から頂点へ反時計まわりにコマ移動させる。
4. それぞれが移動させた後のコマの位置によって、下の表のⅠ〜Ⅳのように勝敗をきめることとする。

	太郎さんが移動させた後のコマの位置	次郎さんが移動させた後のコマの位置	勝敗
Ⅰ	頂点B	頂点B	引き分け
Ⅱ	頂点B	頂点B以外	太郎さんの勝ち
Ⅲ	頂点B以外	頂点B	次郎さんの勝ち
Ⅳ	頂点B以外	頂点B以外	引き分け

例えば、太郎さんが2の数字が書かれたカードを取り出したとき、太郎さんはコマをA→B→Cと移動させます。次に次郎さんが1の数字が書かれたカードを取り出したとき、次郎さんはコマをC→Dと移動させます。この場合は、太郎さんが移動させた後のコマは頂点Cにあり、次郎さんが移動させた後のコマは頂点Dにあるので、Ⅳとなり引き分けとなります。

2人は、太郎さんが勝つ確率と、次郎さんが勝つ確率をそれぞれ求めました。その結果から、この【ゲーム】では、先にカードを取り出す人と、後からカードを取り出す人とでは、勝ちやすさに違いがないことがわかりました。

さらに、【ゲーム】中の<ルール>の2. だけを下の2′.にかえた新しいゲームでも、カードを取り出す順番によって勝ちやすさに違いがないかを調べることにしました。

2′. 太郎さんは、取り出したカードを袋に戻さず、次郎さんに交代する。

この新しいゲームにおいて、先にカードを取り出す人と、後からカードを取り出す人とでは、勝ちやすさに違いはありますか。下のア〜ウの中から正しいものを1つ選び、その記号を書きなさい。また、それが正しいことの理由を、確率を用いて説明しなさい。

ア先にカードを取り出す人と後からカードを取り出す人とでは、勝ちやすさに違いはない。
イ先にカードを取り出す人が勝ちやすい。
ウ後からカードを取り出す人が勝ちやすい。

2022年大問6-(2)

解法

太郎さんが袋の中からカードを取り出せるのは\( \ 4 \ \)通り、
次郎さんが袋の中からカードを取り出せるのは\( \ 3 \ \)通りなので、
2人が袋の中からカードを取り出す場合の数は\( \ 4\times 3=12 \ \) 通りである。

2人が取り出すカードの組み合わせは以下の表の通り。
黒い数字はカードに書かれた数字を表し、青いアルファベットは、コマの位置を表す。
赤い丸は勝者を示し、赤いバツは敗者を示す。
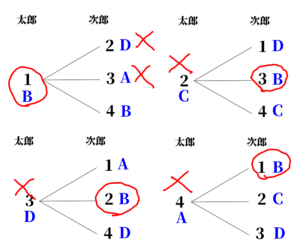表によると、太郎さんが勝つのは\( \ 2 \ \)通り、次郎さんが勝つのは\( \ 3 \ \)通りである。
これにより太郎さんが勝つ確率は \( \ \displaystyle\frac{1}{6} \ \)、次郎さんが勝つ確率は \( \ \displaystyle\frac{1}{4} \ \)であるから、
正しい選択肢は、「ウ後からカードを取り出す人が勝ちやすい。」となる。

Lukia

カードの選択肢が多いから、太郎さんのほうが有利なのかな？と思ったら、次郎さんが勝つ確率のほうが高くなりましたね。
次郎さんが勝ちやすい理由は、次郎さんがカードを取り出す前に、太郎さんがコマを進めてくれているからなんですね。
太郎さんがコマを進めている（進めすぎて頂点Aに戻る）から、次郎さんは、チョイ足しすることで、頂点Bにコマを置ける可能性が増えるんです。

ルールによっては、順番が勝敗に大きく関わることもあることが学べるよい問題でした。