一次方程式で距離を求める【粗忽な大人、高校入試問題を解く〜それ、誤答です！〜】
読了時間: 約2分2秒
広島県公立高校入試の2022年、2021年、2020年の数学の問題を解いてみました。深い読解能力と素早い処理能力が必要とされる問題になっているな。と感じました。
3ヶ年分の問題のうち、私がおっちょこちょいなことをしたり、ツメが甘くて間違えた問題について解き直してみようと思います。
問題
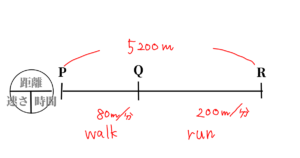
Aさんは、P地点から\( \ 5200 \ \)m離れたQ地点までウォーキングとランニングをしました。P地点から途中のR地点までは分速\( \ 80 \ \)mでウォーキングをし、R地点からQ地点までは分速\( \ 200 \ \)mでランニングをしたところ、全体で\( \ 35 \ \)分かかりました。P地点からR地点までの道のりとR地点からQ地点までの道のりは、それぞれ何mですか。なお、答えを求める過程も分かるように書きなさい。
2020年大問2-(3)
2020年大問2-(3)
解法
パート1：ウォーキングした時間をxとおく場合
ウォーキングをした時間を\( \ x \ \)分とする。
ランニングをした時間は、\( \ 35-x \ \)分と表せる。
$$\begin{align}80x+200\left( 35-x\right)=&5200 \\\\ 80x+7000-200x=&5200 \\\\ -120x=&-1800\\\\ x=&15 \end{align}$$ PR地点は
\( \ 80\times 15=1200 \ \)
RQ地点は
\( \ 5200-1200=4000 \ \)
パート2：ウォーキングした距離をxとおく場合
ウォーキングをした距離を\( \ x \ \)mとする。ランニングをした距離は\( \ 5200-x \ \)mと表せる。
ウォーキングとランニングをした時間は合わせて\( \ 35 \ \)分なので
$$\begin{align}\frac{x}{80}+\frac{5200-x}{200}=&35 \\\\ 両辺を&400倍する \\\\ 5x+2\left( 5200-x\right)=&35\times 400\\\\ 5x+10400-2x=&14000\\\\ 3x=&3600\\\\ x=&1200 \end{align}$$PR地点は
\( \ 1200 \ \)
RQ地点は
\( \ 5200-1200=4000 \ \)
パート1で解き、これだけを載せる予定でしたが、求めるのは距離ですので、最後にもうひと手間かけて、距離を求める必要があります。
そこで、ウォーキングする距離を\( \ x \ \)として、方程式を解けばズバリ答えがでるパート2でも解いてみました。
1問あたり3分弱で解かねばならないので、パート1で解きはじめてしまったら、そのまま解くようにしましょう。
そこで、ウォーキングする距離を\( \ x \ \)として、方程式を解けばズバリ答えがでるパート2でも解いてみました。
1問あたり3分弱で解かねばならないので、パート1で解きはじめてしまったら、そのまま解くようにしましょう。
こたえ
PR地点:\( \ 1200 \ \)m
RQ地点:\( \ 4000 \ \)m
粗忽な大人、高校入試問題を解く〜それ、誤答です！〜の記事一覧
https://makelemonadejp.com/entrance-exam-for-public-high-sch...共有:
プロフィール
Author Profile