複数の文字を1つの文字に統一する【粗忽な大人、高校入試問題を解く〜それ、誤答です!〜】

読了時間: 約3分24秒
広島県公立高校入試の2022年、2021年、2020年の数学の問題を解いてみました。深い読解能力と素早い処理能力が必要とされる問題になっているな。と感じました。
3ヶ年分の問題のうち、私がおっちょこちょいなことをしたり、ツメが甘くて間違えた問題について解き直してみようと思います。
問題
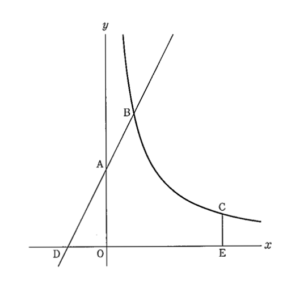
下の図のように、\( \ y \ \)軸上に点\( \ \mathrm{A} \ \)があり、関数\( \ y=\displaystyle\frac{a}{x} \ \)のグラフ上に、\( \ y \ \)座標が\( \ 5 \ \)より大きい範囲で動く点\( \ \mathrm{B} \ \)と\( \ y \ \)座標が\( \ 2 \ \)である点\( \ \mathrm{C} \ \)があります。直線\( \ \mathrm{AB} \ \)と\( \ x \ \)軸との交点を\( \ \mathrm{D} \ \)とします。また、点\( \ \mathrm{C} \ \)から\( \ x \ \)軸に垂線を引き、\( \ x \ \)軸との交点を\( \ \mathrm{E} \ \)とします。ただし、\( \ a \gt 0 \ \)とします。
 \( \ \mathrm{DA}=\mathrm{AB},\mathrm{DE}=9 \ \)となるとき、\( \ a \ \)の値を求めなさい。
\( \ \mathrm{DA}=\mathrm{AB},\mathrm{DE}=9 \ \)となるとき、\( \ a \ \)の値を求めなさい。
2021年大問4-(2)
 \( \ \mathrm{DA}=\mathrm{AB},\mathrm{DE}=9 \ \)となるとき、\( \ a \ \)の値を求めなさい。
\( \ \mathrm{DA}=\mathrm{AB},\mathrm{DE}=9 \ \)となるとき、\( \ a \ \)の値を求めなさい。2021年大問4-(2)
解法
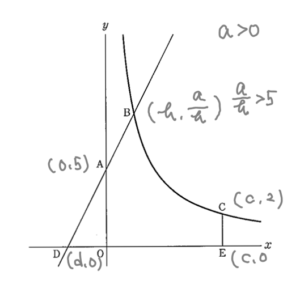 点\( \ \mathrm{B} \ \)の\( \ x \ \)座標を\( \ b \ \),点\( \ \mathrm{C} \ \)の\( \ x \ \)座標を\( \ c \ \),点\( \ \mathrm{D} \ \)の\( \ x \ \)座標を\( \ d \ \)とする。
点\( \ \mathrm{B} \ \)の\( \ x \ \)座標を\( \ b \ \),点\( \ \mathrm{C} \ \)の\( \ x \ \)座標を\( \ c \ \),点\( \ \mathrm{D} \ \)の\( \ x \ \)座標を\( \ d \ \)とする。
(\( \ b,c,d \ \)は実数であり、特に\( \ b \gt 0 \ \),\( \ c \gt 0 \ \),\( \ d \lt 0 \ \))
\( \ \mathrm{DA}=\mathrm{DB} \ \)より、点\( \ \mathrm{A} \ \)は、2点\( \ \mathrm{D},\mathrm{B} \ \)の中点であるから、
$$\begin{align}\frac{b+d}{2}=&0 \\\\ b=&-d \ \cdots \ ①\end{align}$$ $$\begin{align}\frac{0+\displaystyle\frac{a}{b}}{2}=&5 \\\\ \frac{a}{b}=&10 \\\\ a=&10b \ \cdots \ ② \end{align}$$
\( \ 2=\displaystyle\frac{a}{x} \ \) より \( \ c=\displaystyle\frac{a}{2} \ \cdots \ ③ \ \)

さて、ここから\( \ a \ \)の値を求めるのですが、2通りの解き方をご紹介します。
パート1:bに統一しておいてからaを求める
\( \ \mathrm{DE}=9 \ \)より、\( \ c-d=9 \ \)が成り立つ。
\( \ \displaystyle\frac{a}{2}-\left( -b\right)=9 \ \)
\( \ a+2b=18 \ \)
\( \ 10b+2b=18 \ \)
\( \ b=\displaystyle\frac{3}{2} \ \)
\( \ a=10b=10\times \displaystyle\frac{3}{2}=15 \ \)
パート2:aに統一しておいてから求める
\( \ b=\displaystyle\frac{a}{10} \ \)\( \ d=-b=-\displaystyle\frac{a}{10} \ \)
\( \ c=\displaystyle\frac{a}{2} \ \)
\( \ \mathrm{DE}=9 \ \)より
\( \ c-d=9 \ \)
\( \ \displaystyle\frac{a}{2}+\displaystyle\frac{a}{10}=9 \ \)
\( \ 5a+a=90 \ \)
\( \ 6a=90 \ \)
\( \ a=15 \ \)

\( \ a \ \)の求め方について、2つのパターンで求めてみました。
どちらで答えるかはご自身の性格に基づいたらよいかと思います。
パート1は、始めに楽をするが、最後まで気を抜かないタイプ。答えるのは\( \ a \ \)の値なのに、\( \ b \ \)を答えて安心してしまうようなおっちょこちょいの方は向きません。
パート2は、始めにひと手間をかけて、最後に楽をするタイプです。
解答作成をするスペースの最後の方に「\( \ a= \ \)」って書いておくとパート1でもおっちょこちょいをせずに済みそうですね。
どちらで答えるかはご自身の性格に基づいたらよいかと思います。
パート1は、始めに楽をするが、最後まで気を抜かないタイプ。答えるのは\( \ a \ \)の値なのに、\( \ b \ \)を答えて安心してしまうようなおっちょこちょいの方は向きません。
パート2は、始めにひと手間をかけて、最後に楽をするタイプです。
解答作成をするスペースの最後の方に「\( \ a= \ \)」って書いておくとパート1でもおっちょこちょいをせずに済みそうですね。
こたえ
\( \ a=15 \ \)
粗忽な大人、高校入試問題を解く〜それ、誤答です!〜の記事一覧
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません