三角錐とベクトル(その3)【大学入学共通テスト2023年数学ⅡB】

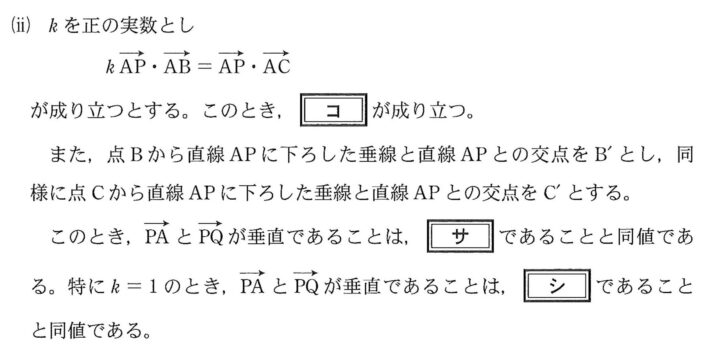
(3)-(ⅰ) より
\( \ \overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{AB}}=\vert \overrightarrow{\mathrm{AP}} \vert \vert \overrightarrow{\mathrm{AB}} \vert \cos \theta \ \)
\( \ \overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{AC}}=\vert \overrightarrow{\mathrm{AP}} \vert \vert \overrightarrow{\mathrm{AC}} \vert \cos \theta \ \) であるから、
$$\begin{align}k\overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{AB}}=&\overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{AC}} \\\\ k\vert \overrightarrow{\mathrm{AP}} \vert \vert \overrightarrow{\mathrm{AB}} \vert \cos \theta=&\vert \overrightarrow{\mathrm{AP}} \vert \vert \overrightarrow{\mathrm{AC}} \vert \cos \theta \\\\ {\color{#0004fc}{k\vert \overrightarrow{\mathrm{AB}} \vert=}}&{\color{#0004fc}{\vert \overrightarrow{\mathrm{AC}} \vert}} \end{align}$$ 
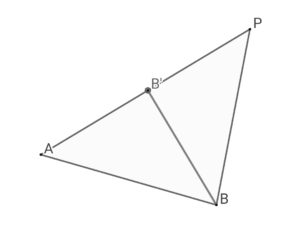 \( \ \vert \overrightarrow{\mathrm{AB}} \vert \cos \theta+\vert \overrightarrow{\mathrm{AC}} \vert \cos \theta=\vert \overrightarrow{\mathrm{AP}} \vert \ \)
\( \ \vert \overrightarrow{\mathrm{AB}} \vert \cos \theta+\vert \overrightarrow{\mathrm{AC}} \vert \cos \theta=\vert \overrightarrow{\mathrm{AP}} \vert \ \)
と
\( \ k\vert \overrightarrow{\mathrm{AB}} \vert =\vert \overrightarrow{\mathrm{AC}} \vert \ \) より
$$\begin{align}\vert \overrightarrow{\mathrm{AB}} \vert \cos \theta+\vert \overrightarrow{\mathrm{AC}} \vert \cos \theta=&\vert \overrightarrow{\mathrm{AP}} \vert \\\\ \vert \overrightarrow{\mathrm{AB}} \vert \cos \theta+k\vert \overrightarrow{\mathrm{AB}} \vert \cos \theta=&\vert \overrightarrow{\mathrm{AP}} \vert \\\\ \left( 1+k\right)\vert \overrightarrow{\mathrm{AB}} \vert \cos \theta=&\vert \overrightarrow{\mathrm{AP}} \vert\\\\ \left( 1+k\right)\vert \overrightarrow{\mathrm{AB}} \vert\times \frac{\vert \overrightarrow{\mathrm{AB’}} \vert}{\vert \overrightarrow{\mathrm{AB}} \vert}=&\vert \overrightarrow{\mathrm{AP}} \vert\\\\ \left( 1+k\right)\vert \overrightarrow{\mathrm{AB’}} \vert=&\vert \overrightarrow{\mathrm{AP}} \vert\end{align}$$
点\( \ \mathrm{B’} \ \)は、線分\( \ \mathrm{AP} \ \)を\( \ 1:k \ \)に内分する。
 \( \ \overrightarrow{\mathrm{AB}}=\displaystyle\frac{1}{k}\vert \overrightarrow{\mathrm{AC}} \vert \ \) より
\( \ \overrightarrow{\mathrm{AB}}=\displaystyle\frac{1}{k}\vert \overrightarrow{\mathrm{AC}} \vert \ \) より
$$\begin{align}\vert \overrightarrow{\mathrm{AB}} \vert \cos \theta+\vert \overrightarrow{\mathrm{AC}} \vert \cos \theta=&\vert \overrightarrow{\mathrm{AP}} \vert\\\\ \frac{1}{k}\vert \overrightarrow{\mathrm{AC}} \vert \cos \theta+\vert \overrightarrow{\mathrm{AC}} \vert \cos \theta=&\vert \overrightarrow{\mathrm{AP}} \vert \\\\ \left( 1+\frac{1}{k}\right)\vert \overrightarrow{\mathrm{AC}} \vert \cos \theta=& \vert \overrightarrow{\mathrm{AP}} \vert \\\\ \left( 1+\frac{1}{k}\right)\vert \overrightarrow{\mathrm{AC}} \vert\times \frac{\vert \overrightarrow{\mathrm{AC’}} \vert}{\vert \overrightarrow{\mathrm{AC}} \vert}=&\vert \overrightarrow{\mathrm{AP}} \vert\\\\ \left( 1+\frac{1}{k}\right)\vert \overrightarrow{\mathrm{AC’}} \vert=&\vert \overrightarrow{\mathrm{AP}} \vert\end{align}$$
点\( \ \mathrm{C’} \ \)は、線分\( \ \mathrm{AP} \ \)を\( \ k:1 \ \)に内分する。
\( \ \overrightarrow{\mathrm{PA}} \ \)と \( \ \overrightarrow{\mathrm{PQ}} \ \)が垂直であることは、
\( \ \mathrm{{\color{#0004fc}{B’}}} \ \)と\( \ \mathrm{{\color{#0004fc}{C’}}} \ \) が線分\( \ \mathrm{{\color{#0004fc}{AP}}} \ \)をそれぞれ\( \ {\color{#0004fc}{1:k}} \ \) と \( \ {\color{#0004fc}{k:1}} \ \) に内分する点 であることと同値である。
 以下の記事一覧に他のボリュームのブログカードを載せています。
以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。











ディスカッション
コメント一覧
まだ、コメントがありません