三角関数の値の大小関係（その3）【大学入学共通テスト2023年数学ⅡB】

2023年1月25日三角関数,大学入学共通テスト

\( \ 0 \leqq x \leqq \pi \ \) のとき、\( \ \sin 3x \gt \sin 4x\quad \cdots \ {\rm{ⅰ}} \ \) かつ \( \ \sin 4x \gt \sin 2x\quad \cdots \ {\rm{ⅱ}} \ \) が成り立つ \( \ x \ \) の範囲を求める。

（ⅰ）
(3)より、
\( \ \displaystyle\frac{ \pi }{ 7 } \lt x \lt \displaystyle\frac{3}{7}\pi \ , \ \displaystyle\frac{5}{7}\pi \lt x \leqq \pi \ \)

（ⅱ）
\( \ 2x=X \ \) とする。
\( \ \sin 4x-\sin 2x \gt 0 \ \)
\( \ \sin 2X-\sin X=2\sin X\left( 2\cos X-1\right) \gt 0 \ \)
\( \ 0 \leqq x \leqq \pi\displaystyle \ \)
\( \ 0 \leqq 2x \leqq 2\pi \ \)
\( \ 0 \leqq X \leqq 2\pi \ \)

(2)より
\( \ 0 \lt X \lt \displaystyle\frac{ \pi }{ 3 } \ , \ \pi \lt X \lt \displaystyle\frac{5}{3}\pi \ \)
すなわち
\( \ 0 \lt x \lt \displaystyle\frac{ \pi }{ 6 } \ , \ \displaystyle\frac{ \pi }{ 2 } \lt x \lt \displaystyle\frac{5}{6}\pi \ \)

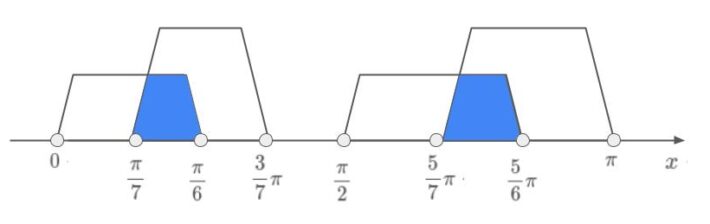
（ⅰ）と（ⅱ）より
\( \ \displaystyle\frac{ \pi }{ 7 } \lt x \lt \displaystyle\frac{ \pi }{ {\color{#0004fc}{6}} } \ , \ \displaystyle\frac{5}{7}\pi \lt x \lt \displaystyle{\color{#0004fc}{\frac{5}{6}}}\pi \ \)

Lukia

(4)の問題が解けるかどうかは、
\( \ \sin 3x \gt \sin 4x \gt \sin 2x \ \) をふたつの不等式に分けられるかどうかにかかっていますね。その後、
（ⅰ）は(3)の否定、
（ⅱ）は、\( \ 2x=X \ \) とおけば、(2)をそっくり使って解くことができます。

以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。

大学入学共通テスト2023年数学ⅡBの記事一覧

2023年大学入学共通テストの数学2Bの問題を解いてみました。

 https://makelemonadejp.com/common-test-for-university-admiss...

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。