微分と積分（その3）【大学入学共通テスト2021年数学ⅡB】

2023年2月14日大学入学共通テスト,微分と積分

$$\begin{align}h\left( x\right)=&f\left( x\right)-g\left( x\right) \\\\ =&ax^3+bx^2 \\\\ =&x^2\left( ax+b\right) \end{align}$$

\( \ h\left( x\right)=0 \ \) となるのは、\( \ x=\displaystyle\frac{{\color{#0004fc}{-b}}}{{\color{#0004fc}{a}}} \ , \ {\color{#0004fc}{0}} \ \) のとき。

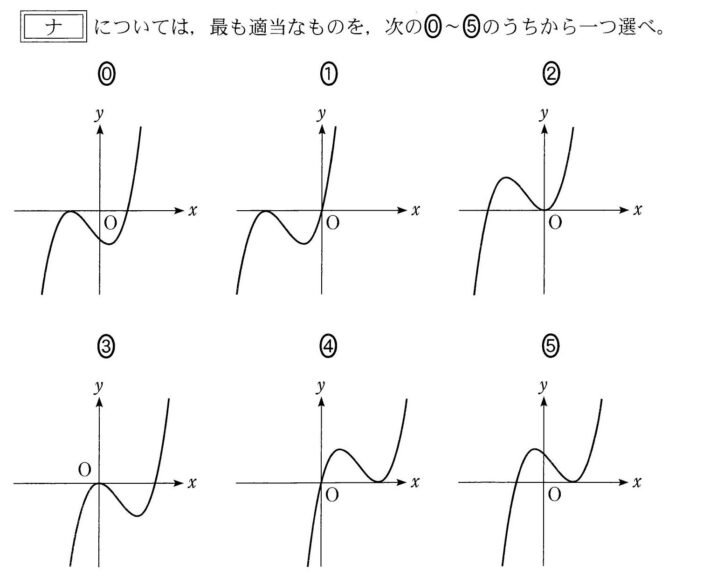
6つのグラフのうち、原点を通っているのは、①、②、③、④の4つ。

さらに、\( \ \displaystyle\frac{-b}{a} \lt 0 \ \) であるから、
\( \ x \lt 0 \ \) の範囲で、\( \ x \ \)軸と交わっている曲線のグラフは①、②の2つ。

\( \ h’\left( x\right)=3ax^2+2bx=0 \ \) より、\( \ x=\displaystyle\frac{{\color{#0004fc}{-2b}}}{{\color{#0004fc}{3a}}} \ \) のとき、極大値をとり、 \( \ x=0 \ \) のとき極小値をとる。

ゆえに正しいグラフは、②

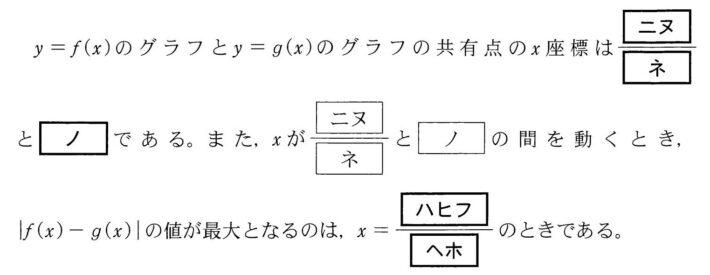
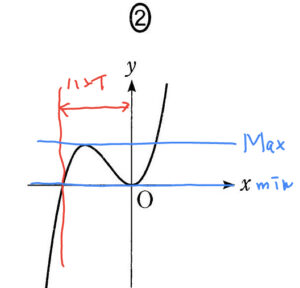求める最大値となるのは、\( \ x=\displaystyle\frac{{\color{#0004fc}{-2b}}}{{\color{#0004fc}{3a}}} \ \) のとき。

以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。

大学入学共通テスト2021年数学ⅡBの記事一覧

2021年大学入学共通テストの数学2Bの問題を解いてみました。

 https://makelemonadejp.com/common-test-for-university-admiss...

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。