表計算ソフトで複利の計算をする(解法動画あり)【ビジネス数学検定2級 合格への道】

読了時間: 約2分27秒
第75回 ビジネス数学検定受検まで あと45日受検勉強を再開した2022年4月18日より27日経過しています。

2022年5月11日に対数を用いて解く問題をご紹介しましたが、
ちょっと引っかかっていました。
対数は高校数学から離れて久しい方が、学び直すにはなかなか大変でしょうし、
ビジネス数学検定のためだけに学び直すというのも、あんまりコスパのよい行為ではありません。
そこで、表計算ソフトを用いての解法を紹介することにしました。
お仕事ではエクセルやスプレッドシートなどの表計算ソフトを多用する場面が多いでしょうから、
ビジネス数学の問題が表計算ソフトで解けるようになれば、実益になりますよね。
問題
以下の表は、G社とS社の、2016年の年間売上高と、過去5年間の年間売上高の平均成長率を表したものです。
今後、両社とも平均成長率で成長を続けるならば、G社の年間売上高がS社の年間売上高を上回るのは何年ですか。
① 2019年
② 2020年
③ 2021年
④ 2022年
⑤ 2023年
| G社 | S社 | |
| 年間売上高 (百万円) |
3,816 | 5,179 |
| 平均成長率 (%) |
5.71 | 0.93 |
今後、両社とも平均成長率で成長を続けるならば、G社の年間売上高がS社の年間売上高を上回るのは何年ですか。
① 2019年
② 2020年
③ 2021年
④ 2022年
⑤ 2023年
初公開!解法動画
このたび、初の試みとして、解法動画を作成してみました。何度か撮り直したものの、拙い点は多々あります。ご了承くださいね。
解法(文字による)
G社の予想売上高が、S社の予想売上高を上回るのは、2019年から2023年のいずれかだ。とヒントが出されているようなものなので、これを利用します。
「年」の列を作り、数字を入力します。
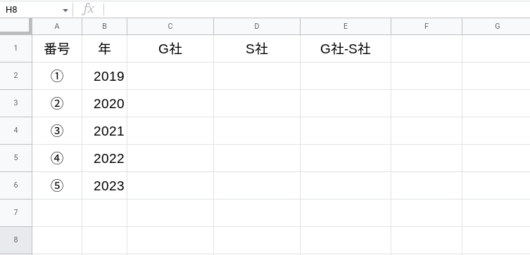 各年のG社の予想売上高を求める数式を入力します。
各年のG社の予想売上高を求める数式を入力します。
C2セルに
=3816*1.0571^(B2-2016)
と入力し、エンターキーを押して確定します。
これは、\( \ =3816\times 1.0571^\left( \rm{B2セル}-2016\right)\ \) という数式を表しています。
「^」は累乗の記号です。
たとえば、3^2は、\( \ 3^2=3\times 3=9 \ \)の意味です。
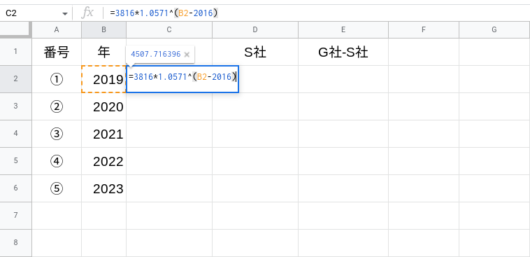

ここで重要なのが「^(B2-2016)」の表記です。
もし、カッコなしの「^B2-2016」とすると、2019乗して、2016を引く。という意味になってしまいます。
本来は、2016年からの経過年数を入力したいのです。
たとえば、2019年は3年経過していますから、各年度ごとにいちいち「^3」とか「^4」とか入れてもいいのですが、めんどくさいでしょう?
一度だけ正確な数式を立ててしまえば、自動入力してくれるのが表計算ソフトのいいところです。しっかり甘えましょう。
もし、カッコなしの「^B2-2016」とすると、2019乗して、2016を引く。という意味になってしまいます。
本来は、2016年からの経過年数を入力したいのです。
たとえば、2019年は3年経過していますから、各年度ごとにいちいち「^3」とか「^4」とか入れてもいいのですが、めんどくさいでしょう?
一度だけ正確な数式を立ててしまえば、自動入力してくれるのが表計算ソフトのいいところです。しっかり甘えましょう。
C3セル以下は、C2セルの右下をダブルクリックすれば自動入力されます。
(Googleスプレッドシートの場合は、「自動入力」されます。)
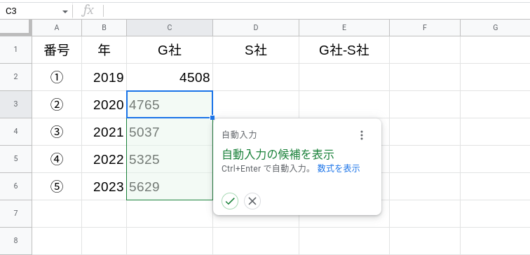 S社の各年の予想売上高についても、同様に数式を入力します。
S社の各年の予想売上高についても、同様に数式を入力します。
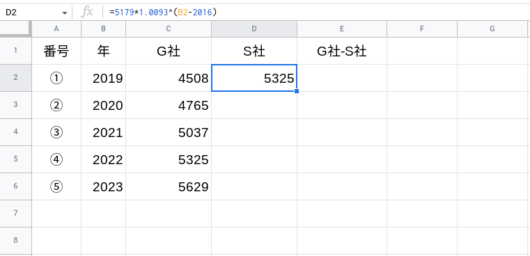 E2セルに、
E2セルに、
=C2-D2
と入力します。
そして、2023年までこの式を入力します。
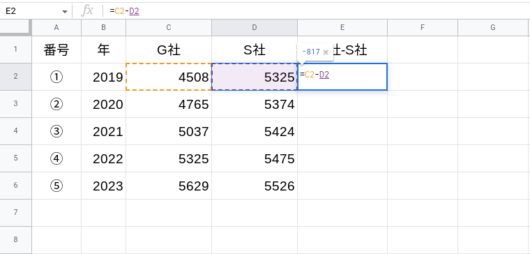 すると、結果は以下の通り。
すると、結果は以下の通り。
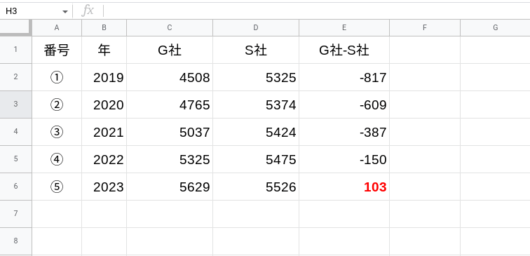 2019年から2022年までは、マイナスがついていますので、G社の予想売上高がS社のそれよりも下回っているということになります。
2019年から2022年までは、マイナスがついていますので、G社の予想売上高がS社のそれよりも下回っているということになります。
しかし、徐々に差は縮まっていることがわかりますね。
そして、2023年、マイナスはついていません。つまり、2023年にG社の予想売上高はS社のそれを追い抜いたことがわかります。
よって答えは、⑤の2023年ということになります。
こたえ
⑤ 2023年









ディスカッション
コメント一覧
まだ、コメントがありません