3つの集合問題はカルノー図で簡単解決！（問題編）【ビジネス数学検定2級 合格への道】

2022年5月4日2023年1月31日SPI能力検査（非言語分野）,ビジネス数学検定,集合と論理3つの集合問題をカルノー図で解く,SPI能力検査(非言語分野),ビジネス数学検定2級

第75回 ビジネス数学検定受検まで あと55日
受検勉強を再開した2022年4月18日より17日経過しています。
ビジネス数学検定2級の公式問題集の中で、ここは数学の知識があるほうが解きやすいなという問題について、
いくつか紹介してみたいと思います。

＜実践＞ビジネス数学検定2級 [ （公財）日本数学検定協会 ] 価格：1320円（税込、送料無料) (2022/4/23時点) 楽天で購入

解法

カルノー図をかいて考えていきます。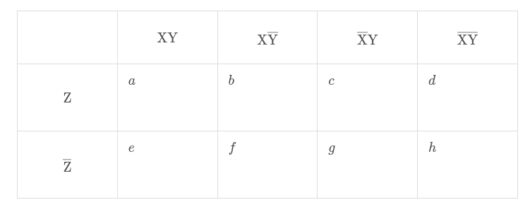 $$\begin{align}\mathrm{X}+\mathrm{Y}+\mathrm{Z}=&3a+2\left( b+c+e\right)+\left( d+f+g\right) \\\\ =&188+151+100 \\\\ =&439 \ \cdots\quad ① \end{align}$$

2つの資格を取得している人のことを考えるとき、3つ目の資格を取得しているかどうかは問題としません。
たとえば、「資格\( \ \mathrm{X} \ \)を取得している人で 資格\( \ \mathrm{Y} \ \)も取得している人」の\( \ 98 \ \)人の中には、資格\( \ \mathrm{Z} \ \)を取得している人（カルノー図で\( \ a \ \)にあたる）も、資格\( \ \mathrm{Z} \ \)を取得していない人（カルノー図で\( \ e \ \)にあたる）も含まれていると考えます。

同様に考えて、
$$\begin{align}a+e=&98 \\\\ a+c=&41 \\\\ a+b=&56\\\\ 辺々&加えて\\\\ 3a+\left( b+c+e\right)=&195 \ \cdots② \end{align}$$
全従業員のうち\( \ 65 \ \)人はいずれの資格も取得していないので、
$$\begin{align}\mathrm{X}\cup\mathrm{Y}\cup\mathrm{Z}=\mathrm{U}-h=&a+\left( b+c+e\right)+\left( d+f+g\right) \\\\ =&326-65 \\\\ =&261 \ \cdots\quad ③ \end{align}$$

ここで、\( \ \alpha=b+c+e \ , \ \beta=d+f+g \ \) とする。
整理すると、
$$\begin{align}3a+2\alpha+\beta=&439 \ \cdots\quad ① \\\\ 3a+\alpha=&295 \ \cdots\quad ②\\\\ a+\alpha+\beta=&261 \ \cdots\quad ③ \end{align}$$ ①-② より
\( \ \alpha+\beta=244 \ \cdots\quad ④ \ \)
④を③に代入して、
$$\begin{align}a+244=&261 \\\\ a=&17 \end{align}$$

いかがですか？一見複雑そうな表から、サクサクと人数を求めることができました。
この3つの集合の問題は、もっと複雑なものもありますが、ビジネス数学検定では1問あたり2分弱で解かないといけないので、おそらくこのぐらいの問題が出題されるのではないかと思います。
同じ問題でいいですから、カルノー図の書き方と式を覚え、スムーズに解答できるようになっておきましょう。

こたえ

\( \ 17 \ \)人

ビジネス数学検定2級 合格への道の記事一覧

Leave This Blank:Leave This Blank Too:Do Not Change This:

メールアドレス：

 

よろしければ、アンケートに御協力ください。
アンケートでは、お読みになったタイトルをうかがいますので、御確認ください。
この記事のタイトルは『 3つの集合問題はカルノー図で簡単解決！（問題編）』です。