固定費のジレンマ（損益分岐点への影響）

2022年6月10日2023年1月31日ビジネス数学検定,中学数学ビジネス数学検定2級

損益分岐点は2つの直線の交点

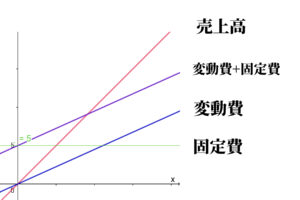損益分岐点は、売上高を表す赤い直線と、変動費+固定費を表す紫の直線の交点です。
売上数量を \( \ x \ \) ,金額を \( \ y \ \) とします。
販売単価を \( \ a \ \) , 一つあたりの変動費を \( \ b \ \) , 固定費を \( \ c \ \) とします。

売上高は \( \ y=ax \ \)
変動費は \( \ y=bx \ \)
固定費は \( \ y=c \ \)
変動費+固定費は \( \ y=bx+c \ \)

さらに、
損益分岐点の数量は、\( \ x=\displaystyle\frac{c}{\left( a-b\right)}=\displaystyle\frac{\rm{固定費}}{\left( \rm{販売単価}-\rm{変動費}\right)} \ \)
利益は、\( \ y=\left( a-b\right)x-c=\left( \rm{販売単価}-\rm{変動費}\right)x-\rm{固定費} \ \) で求められます。

解法

販売価格を求める

損益分岐点を求めるには、販売価格、変動費（1個あたりの）、固定費がわかっていないといけません。
まずは、販売価格を求めます。
見込み販売数を5万台のときの利益率が20%なので、
$$\begin{align}\rm{利益率}=&\frac{\left( \rm{販売単価}-\rm{変動費}\right)\times \rm{販売数量}-\rm{固定費}}{\rm{売上高}} \\\\ 0.2=&\frac{\left( a-1\right)\times 5\rm{万}^2-3\rm{万}^2}{5a\rm{万}^2} \\\\ 0.2=&\frac{5a-8}{5a}\\\\ a=&5a-8\\\\ a=&2 \end{align}$$

これにより販売価格は2万円であるとわかります。

製造機器の更新後の損益分岐点の販売数量

損益分岐点の販売台数を\( \ x \ \)とする。
また更新後の固定費は9億となる。
$$\begin{align}2x\rm{万}=&x\rm{万}+9\rm{万}^2 \\\\ x\rm{万}=&9\rm{万}^2 \\\\ x=&9万 \end{align}$$
9万台

利益率が20％を超えるのは？

$$\begin{align}\frac{\left( 2-1\right)x\rm{万}-9\rm{万}^2}{2x\rm{万}} \geqq &0.2 \\\\ x\rm{万}-9\rm{万}^2 \geqq &0.4x\rm{万} \\\\ 0.6x \geqq &9\rm{万}\\\\ x \geqq& 15\rm{万} \end{align}$$
15万台

利益率が7万台を販売したときと同じになるのは？

$$\begin{align}\frac{\left( 2-1\right)\times 7-3}{2\times 7}=&\frac{x-9}{2x} \\\\ \frac{4}{14}=&\frac{x-9}{2x} \\\\ 4x=&7x-63\\\\ 3x=&63\\\\ x=&21 \end{align}$$ 21万台

Leave This Blank:Leave This Blank Too:Do Not Change This:

メールアドレス：

 

よろしければ,アンケートに御協力ください。
アンケートでは、お読みになったタイトルをうかがいますので、御確認ください。
この記事のタイトルは『固定費のジレンマ（損益分岐点への影響）』です。