高校数学の絶対値の問題は、グラフでイメージしよう。

2018年8月25日2023年1月15日数と式実用数学技能検定（数学検定 数検),数検準2級

[mathjax]
$$\begin{align}&-3 \lt x \lt 0 のとき、\\ &3\sqrt{x^2-4x+4}-2\sqrt{x^2+6x+9}+4\sqrt{x^2} を簡単にせよ。\end{align}$$
$$\begin{align}与式&=3\sqrt{\left( x-2\right)^2}-2\sqrt{\left( x+3\right)^2}+4\sqrt{x^2}\\&=3\color{blue}{\vert x-2 \vert}-2\color{green}{\vert x+3 \vert}+4\color{red}{\vert x \vert} \end{align}$$
$$\begin{align} 以下に　y&=\color{blue}{\vert x-2 \vert} \\y&=\color{green}{\vert x+3 \vert} \\ y&=\color{red}{\vert x \vert}　を示す。 \end{align}$$

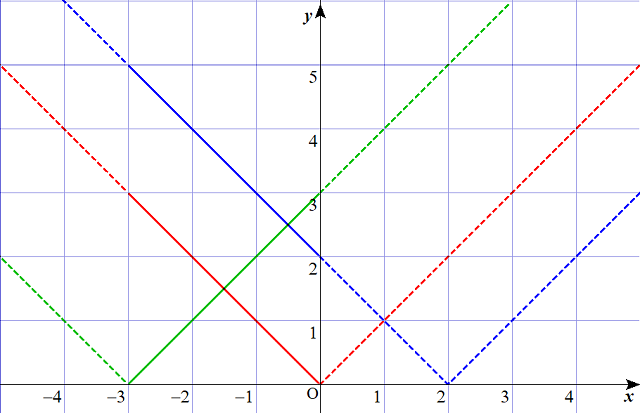
$$\begin{align}&-3 \lt x \lt 0　において、\\ y&=\color{blue}{-x+2} \\ y&=\color{green}{x+3}\\ y&=\color{red}{-x} （それぞれ実線部分）であるから、 \end{align}$$
$$\begin{align}与式&= 3\color{blue}{\left( -x+2\right)}-2\color{green}{\left( x+3\right)}+4\color{red}{\left( -x\right)}\\ &=-3x+6-2x-6-4x \\ &=-9x \end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。