高校数学の「三角形の内心とベクトル」に関する問題を解いてみる。【Yahoo!知恵袋より】

2022年7月21日2023年1月8日ベクトル

解法

三角形の内心はそれぞれの角の二等分線の交点である。
また、角の二等分線は、対辺を、その角をなす2つの線分の比に内分する。

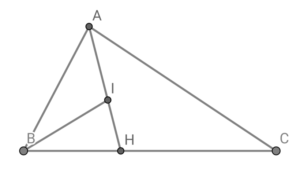\( \ \angle \mathrm{BAC} \ \) の二等分線と辺\( \ \mathrm{BC} \ \) との交点を\( \ \mathrm{H} \ \)とする。
\( \ \mathrm{AB}:\mathrm{AC}=\mathrm{BH}:\mathrm{CH} \ \)より
\( \ \mathrm{BH}=\displaystyle\frac{5}{13}\times 9=\displaystyle\frac{45}{13} \ \)

同様に
\( \ \mathrm{BA}:\mathrm{BH}=\mathrm{AH}:\mathrm{IH} \ \)より
\( \ \mathrm{AH}:\mathrm{IH}=13:9 \ \)
すなわち \( \ \overrightarrow{\mathrm{AI}}=\displaystyle\frac{13}{13+9}\overrightarrow{\mathrm{AH}} \ \)

\( \ \overrightarrow{\mathrm{AH}}=\displaystyle\frac{1}{13}\left( 8\vec{b}+5\vec{c}\right) \ \) より
\( \ \overrightarrow{\mathrm{AI}}=\displaystyle\frac{13}{22}\cdot \displaystyle\frac{1}{13}\left( 8\vec{b}+5\vec{c}\right)=\displaystyle\frac{1}{22}\left( 8\vec{b}+5\vec{c}\right) \ \)

こたえ

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。