四角形の内角の大きさを求める【粗忽な大人、高校入試問題を解く〜それ、誤答です！〜】
読了時間: 約1分42秒
広島県公立高校入試の2022年、2021年、2020年の数学の問題を解いてみました。深い読解能力と素早い処理能力が必要とされる問題になっているな。と感じました。
3ヶ年分の問題のうち、私がおっちょこちょいなことをしたり、ツメが甘くて間違えた問題について解き直してみようと思います。
問題
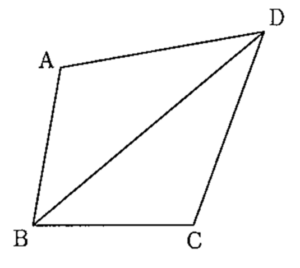上の図のように、四角形\( \ \mathrm{ABCD} \ \)があり、\( \ \mathrm{AB}=\mathrm{BC} \ \),\( \ \mathrm{CD}=\mathrm{DA} \ \)である。\( \ \angle \mathrm{BAD}=110^{\circ} \ \),\( \ \angle \mathrm{CBD}=40^{\circ} \ \)のとき、\( \ \angle \mathrm{ADC} \ \)の大きさは何度か。2022年大問1-(7)
\( \ \angle \mathrm{ADC} \ \)の大きさじゃなくて、\( \ \angle \mathrm{ADB} \ \)の大きさを求めちゃいました。 なんておっちょこちょいなんでしょう。。。
解法
\( \ \triangle \mathrm{ABD} \ \)と\( \ \triangle \mathrm{CBD} \ \)において、
仮定より
\( \ \mathrm{AB}=\mathrm{CB}\cdots \ \)①
\( \ \mathrm{AD}=\mathrm{CD}\cdots \ \)②
\( \ \mathrm{BD}=\mathrm{BD}\cdots \ \)③
①〜③より
三辺の長さがそれぞれ等しいので、\( \ \triangle \mathrm{ABD} \equiv \triangle \mathrm{CBD} \ \)
四角形の内角の和は\( \ 360^{\circ} \ \)であるから、
\( \ \angle \mathrm{ADC}=360^{\circ}-\left( 110^{\circ}+40^{\circ}\right)\times 2=60^{\circ} \ \)
仮定より
\( \ \mathrm{AB}=\mathrm{CB}\cdots \ \)①
\( \ \mathrm{AD}=\mathrm{CD}\cdots \ \)②
\( \ \mathrm{BD}=\mathrm{BD}\cdots \ \)③
①〜③より
三辺の長さがそれぞれ等しいので、\( \ \triangle \mathrm{ABD} \equiv \triangle \mathrm{CBD} \ \)
四角形の内角の和は\( \ 360^{\circ} \ \)であるから、
\( \ \angle \mathrm{ADC}=360^{\circ}-\left( 110^{\circ}+40^{\circ}\right)\times 2=60^{\circ} \ \)
実際の試験では、2つの三角形が合同であることを証明する必要はありません。
問題の難易度を考えないなら、こういう小問を3分弱で解かなければならないので、大問1あたりは、時間をかけずにぱっぱっと処理していく力が求められます。
問題の難易度を考えないなら、こういう小問を3分弱で解かなければならないので、大問1あたりは、時間をかけずにぱっぱっと処理していく力が求められます。
こたえ
\( \ 60^{\circ} \ \)
粗忽な大人、高校入試問題を解く〜それ、誤答です！〜の記事一覧
https://makelemonadejp.com/entrance-exam-for-public-high-sch...共有:
プロフィール
Author Profile
