ねじれの位置にある辺を求める【粗忽な大人、高校入試問題を解く〜それ、誤答です！〜】
読了時間: 約1分9秒
広島県公立高校入試の2022年、2021年、2020年の数学の問題を解いてみました。
深い読解能力と素早い処理能力が必要とされる問題になっているな。と感じました。
3ヶ年分の問題のうち、私がおっちょこちょいなことをしたり、ツメが甘くて間違えた問題について解き直してみようと思います。
問題
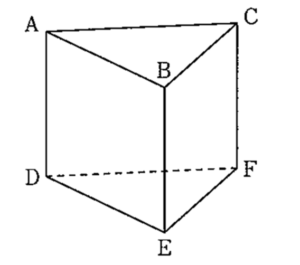上の図のように、2つの底面が\( \ \triangle \mathrm{ABC} \ \)と\( \ \triangle \mathrm{DEF} \ \)である三角柱がある。この三角柱において、辺\( \ \mathrm{AB} \ \)とねじれの位置にある辺を全て答えよ。2022年大問1-(5)
答えは辺\( \ \mathrm{CF} \ \)、辺\( \ \mathrm{DF} \ \)でしょ！と思ったら、辺\( \ \mathrm{EF} \ \)を見落としていました。
おっちょこちょいですね。
おっちょこちょいですね。
解法
ねじれの位置にある辺とは指定された辺に対して平行でない・交わってない位置にある辺を指します。ということは、指定された辺に対して平行な辺・交わっている辺を除外していけば、答えが求められることになりますね。
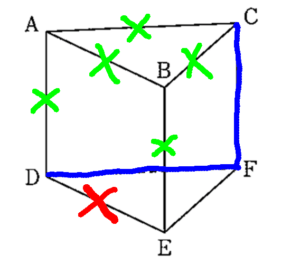
辺\( \ \mathrm{AB} \ \)と平行な辺に赤いバツをし、辺\( \ \mathrm{AB} \ \)と交わっている辺に緑のバツをします。
バツされていない3つの辺（青線）が答えとなります。
こたえ
辺\( \ \mathrm{CF} \ \),辺\( \ \mathrm{EF} \ \),辺\( \ \mathrm{DF} \ \)
粗忽な大人、高校入試問題を解く〜それ、誤答です！〜の記事一覧
https://makelemonadejp.com/entrance-exam-for-public-high-sch...共有:
プロフィール
Author Profile