三角錐とベクトル（その4）【大学入学共通テスト2023年数学ⅡB】
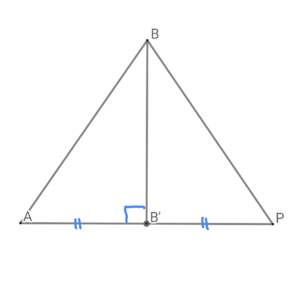
三角形\( \ \mathrm{BAP} \ \)において、線分\( \ \mathrm{BB’} \ \)は線分\( \ \mathrm{AP} \ \)の垂直二等分線であることから、
三角形\( \ \mathrm{BAP} \ \)は、\( \ \mathrm{BA}=\mathrm{BP} \ \)の二等辺三角形である。
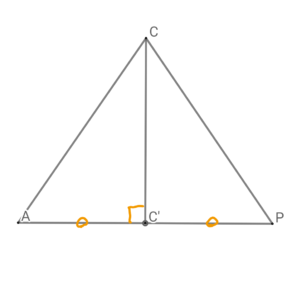三角形\( \ \mathrm{CAP} \ \)において、線分\( \ \mathrm{CC’} \ \)は線分\( \ \mathrm{AP} \ \)の垂直二等分線であることから、
三角形\( \ \mathrm{CAP} \ \)は、\( \ \mathrm{CA=CP} \ \)の二等辺三角形である。
以上より、
特に\( \ k=1 \ \)のとき、\( \ \overrightarrow{\mathrm{PA}} \ \) と \( \ \overrightarrow{\mathrm{PQ}} \ \) が垂直であることは
\( \ {\color{#0004fc}{\triangle \mathrm{PAB}}} \ \) と \( \ {\color{#0004fc}{\triangle \mathrm{PAC}}} \ \) がそれぞれ\( \ {\color{#0004fc}{\mathrm{BP}=\mathrm{BA}}} \ \) , \( \ {\color{#0004fc}{\mathrm{CP}=\mathrm{CA}}} \ \) を満たす二等辺三角形 であることと同値である。
選択肢③ではいけないの？
選択肢②の条件に加えて、
\( \ k=1 \ \) のとき、\( \ \mathrm{AB}=\mathrm{AC} \ \) になりますので、
\( \ \triangle \mathrm{PAB} \ \)と\( \ \triangle \mathrm{PAC} \ \)は合同な三角形であるといえます。
そうなると、選択肢③でもいいような気がしますが、包含関係で確かめてみましょう。
「\( \ \triangle \mathrm{PAB} \ \)と\( \ \triangle \mathrm{PAC} \ \)が選択肢②の条件を満たす二等辺三角形である」ならば、「\( \ \triangle \mathrm{PAB} \ \)と\( \ \triangle \mathrm{PAC} \ \)は合同な三角形である」といえますが、
逆はどうでしょうか。
「二つの三角形が合同」ならば、必ず「二等辺三角形」ですか？
三角形の合同条件を満たす三角形はいろいろあります。二等辺三角形だけではありません。
今回の場合、選択肢②を経て、選択肢③がいえるので、いきなり選択肢③を選んでしまうのは、飛躍しすぎなんですね。
以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。
https://makelemonadejp.com/common-test-for-university-admiss...共有:
プロフィール
