微分と積分（その4）【大学入学共通テスト2023年数学ⅡB】
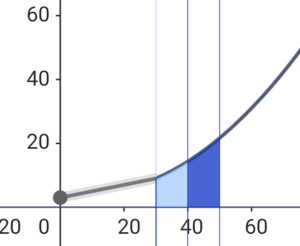\( \ \displaystyle\int_{30}^{40} f\left( x\right) dx \ \) は上図の薄い青で塗りつぶされた部分。
\( \ \displaystyle\int_{40}^{50} f\left( x\right) dx \ \) は上図の濃い青で塗りつぶされた部分。
ゆえに、
\( \ \ \displaystyle\int_{30}^{40} f\left( x\right) dx {\color{#0004fc}{\lt}} \displaystyle\int_{40}^{50} f\left( x\right) dx \ \)
\( \ \mathrm{S}\left( t\right) \ \) が \( \ 400 \ \)に到達したとき、ソメイヨシノは開花するが、
\( \ 0 \ \)日から\( \ 30 \ \)日までで\( \ 180 \ \)、
\( \ 30 \ \)日から\( \ 40 \ \)日までで\( \ 115 \ \)とわかっているので、
\( \ \displaystyle\int_{40}^{50} f\left( x\right) dx \geqq 400-180-115 \ \) になるかどうかを計算する。
$$\begin{align}\left[\frac{1}{300}x^3-\frac{1}{12}x^2+5x\right]_{40}^{50}=&\frac{1}{300}\left[x^3+25x^2+1500x\right]_{40}^{50} \\\\ =&\frac{1}{300}\lbrace 50^3-40^3-25\left( 50^2-40^2\right)+1500\times 10\rbrace \\\\ \fallingdotseq &536.7 \gt 105 \end{align}$$ つまり、\( \ {\color{#0004fc}{40}} \ \)日後より後、かつ\( \ {\color{#0004fc}{50}} \ \)日後より前に開花する。
以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。
https://makelemonadejp.com/common-test-for-university-admiss...共有:
プロフィール
