微分と積分（その2）【大学入学共通テスト2023年数学ⅡB】
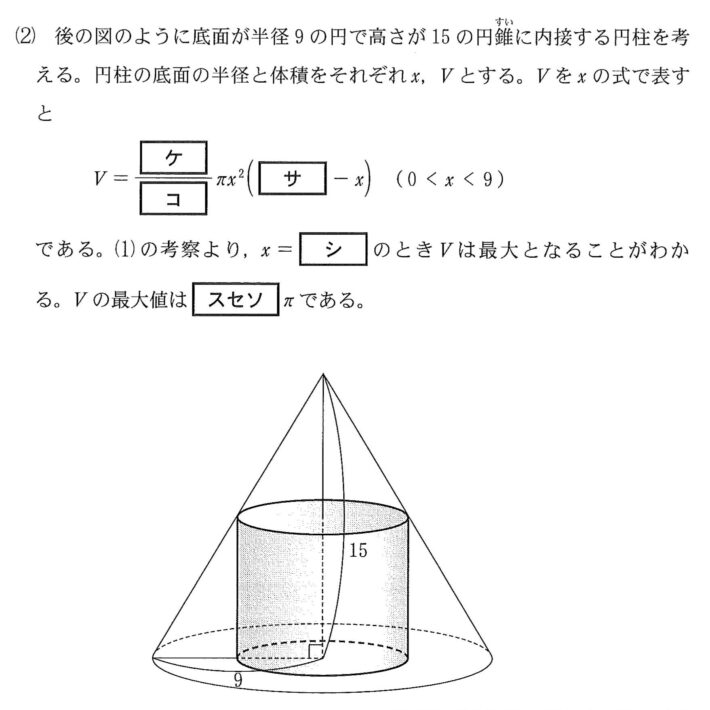円柱の高さを\( \ h \ \)とし、以下のような円錐の断面図をもとに\( \ h \ \)を求める。
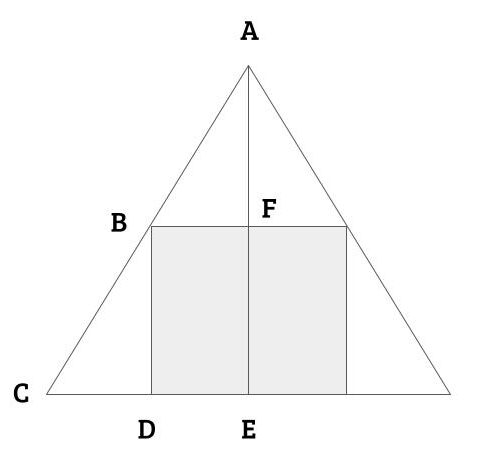
\( \ \triangle \mathrm{ACE} \ \)は、辺\( \ \mathrm{AC} \ \)を斜辺とし、\( \ \mathrm{AE}=15 \ , \ \mathrm{CE}=9 \ \)の直角三角形である。
その面積を\( \ \mathrm{S} \ \) とすると、
\( \ \mathrm{S}=\displaystyle\frac{1}{2}\times 9\times 15=\displaystyle\frac{135}{2} \ \) と表せる。
ここで、\( \ \mathrm{DE}=x \ , \ \mathrm{FE}=h \ \) とすると、\( \ \mathrm{CD}=9-x \ , \ \mathrm{AF}=15-h \ \) と表せる。
\( \ \triangle \mathrm{ACE}=\triangle \mathrm{ABF}+\triangle \mathrm{BCD}+\mathrm{BDEF} \ \) より
$$\begin{align}\frac{1}{2}\times 9\times 15=&\frac{1}{2}x\left( 15-h\right)+\frac{1}{2}\left( 9-x\right)\times h+xh \\\\ 9\times 15=&15x-xh+9h-xh+2xh \\\\ 3\times 15=&3h+5x\\\\ h=&15-\frac{5}{3}x \end{align}$$
ゆえに、円柱の体積は、
$$\begin{align}\mathrm{V}=&x^2\pi\cdot h \\\\ =&x^2\pi\left( 15-\frac{5}{3}x\right)\\\\ =&{\color{#0004fc}{\frac{5}{3}}}x^2\pi\left( {\color{#0004fc}{9}}-x\right) \end{align}$$
\( \ \mathrm{V} \ \) は、（1）の\( \ f\left( x\right) \ \) を\( \ \displaystyle\frac{5}{3}\pi \ \) 倍し、\( \ k=9 \ \) を代入したものに等しい。
ゆえに
\( \ x=\displaystyle\frac{2}{3}\times 9={\color{#0004fc}{6}} \ \) のとき
\( \ \mathrm{V} \ \)の最大値は
$$\begin{align}V=&\frac{5}{3}\pi\times \frac{4}{27}\times 9^3 \\\\ =&{\color{#0004fc}{180}}\pi \end{align}$$
Lukia
断面図で次元を下げて考える発想が出せるかどうかで、解く時間が変わってきそうです。
こういう発想力は、日々の練習がものをいいそうですね。
以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。
https://makelemonadejp.com/common-test-for-university-admiss...共有:
プロフィール