微分と積分（その1）【大学入学共通テスト2023年数学ⅡB】

2023年1月27日大学入学共通テスト,微分と積分

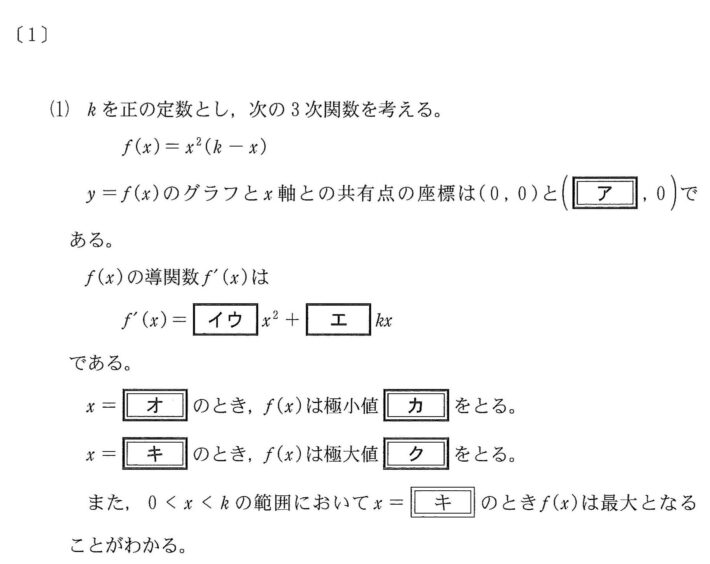
$$\begin{align}f\left( x\right)=&0\\\\ x^2\left( k-x\right)=&0 \\\\ x=&0 \ , \ {\color{#0004fc}{k}} \end{align}$$
$$\begin{align}f'(x)=&\left( x^2\right)^{'}+x^2\left( k-x\right)^{'} \\\\ =&2x\left( k-x\right)-x^2 \\\\ =&{\color{#0004fc}{-3}}x^2+{\color{#0004fc}{2}}kx \end{align}$$
\( \ f'(x)=0 \ \) となるのは、\( \ x=0 \ , \ x=\displaystyle\frac{2}{3}k \ \) のとき。
特に、\( \ k \gt 0 \ \) より増減表は以下の通り。

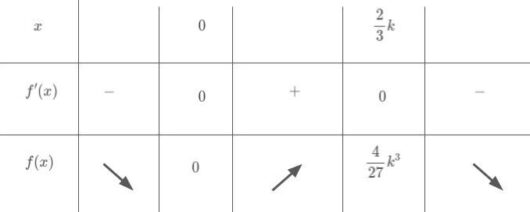
ゆえに、
\( \ x={\color{#0004fc}{0}} \ \) のとき、\( \ f\left( x\right) \ \) は極小値 \( \ {\color{#0004fc}{0}} \ \) をとる。
\( \ x={\color{#0004fc}{\displaystyle\frac{2}{3}k}} \ \) のとき、\( \ f\left( x\right) \ \) は極大値 \( \ {\color{#0004fc}{\displaystyle\frac{4}{27}k^3}} \ \) をとる。

以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。

大学入学共通テスト2023年数学ⅡBの記事一覧

2023年大学入学共通テストの数学2Bの問題を解いてみました。

 https://makelemonadejp.com/common-test-for-university-admiss...

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。