指数と対数【大学入学共通テスト2023年数学ⅡB】

2023年1月26日大学入学共通テスト,指数と対数

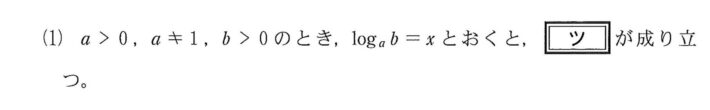
\( \ {\color{#0004fc}{a^x=b}} \ \)

---

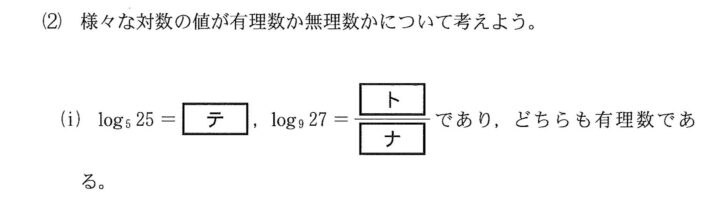
\( \ \log_{5}25=\log_{5}5^2={\color{#0004fc}{2}} \ \)

\( \ \log_{9}27=\displaystyle\frac{\log_{3}27}{\log_{3}9}=\displaystyle\frac{3\log_{3}3}{2\log_{3}3}=\displaystyle{\color{#0004fc}{\frac{3}{2}}} \ \)

---

$$\begin{align}\log_{2}3=&\frac{p}{q} \\\\ 2^{\frac{p}{q}}=&3 \\\\ 2^{\frac{p}{q}\times q}=&3^q\\\\ {\color{#0004fc}{2^p}}=&{\color{#0004fc}{3^q}} \end{align}$$

---

選択肢0〜3までは、\( \ a \ \)または\( \ b \ \)が、偶数または奇数であっても、他方が偶数であるか奇数であるかが特定されていないので、場合によっては有理数になることもある。
選択肢4は、\( \ 2^x=8 \ \) や\( \ 3^x=9 \ \) のように有理数になる例があるので、不適。
ゆえに、選択肢5の「\( \ {\color{#0004fc}{a}} \ \)と\( \ {\color{#0004fc}{b}} \ \)のいずれか一方が偶数でもう一方が奇数」が正解。
以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。

Leave This Blank:Leave This Blank Too:Do Not Change This:

メールアドレス：