正十二面体とベクトル（その5）【大学入学共通テスト】
読了時間: 約0分40秒
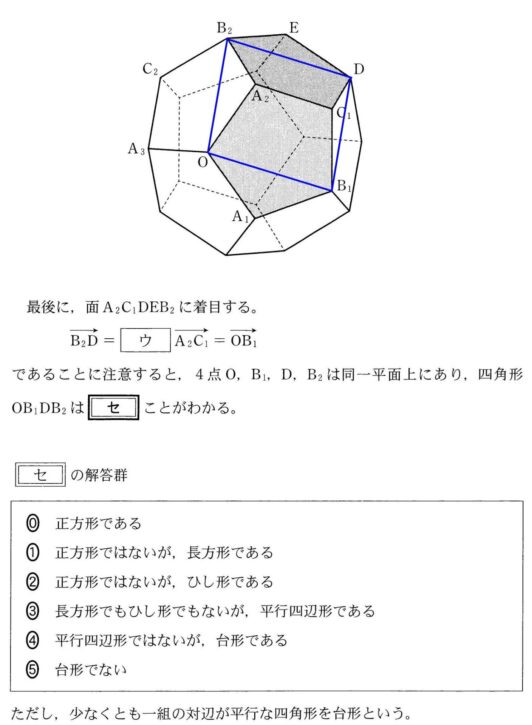
各辺の長さは\( \ a \ \)であり、
\( \ \mathrm{B_2D} \ \)//\( \ \mathrm{OB_1} \ \) , \( \ \mathrm{OB_2} \ \)//\( \ \mathrm{B_1D} \ \)である。
\( \ \overrightarrow{\mathrm{OB_1}}\cdot \overrightarrow{\mathrm{OB_2}}=0 \ \) より、\( \ \mathrm{B_1OB_2}=90^{\circ} \ \)であることと、
平行線の錯角の性質を用いると、
\( \ \mathrm{B_2D} \ \)//\( \ \mathrm{OB_1} \ \) , \( \ \mathrm{OB_2} \ \)//\( \ \mathrm{B_1D} \ \)である。
\( \ \overrightarrow{\mathrm{OB_1}}\cdot \overrightarrow{\mathrm{OB_2}}=0 \ \) より、\( \ \mathrm{B_1OB_2}=90^{\circ} \ \)であることと、
平行線の錯角の性質を用いると、
4つの角はいずれも等しい（直角である）といえる。
以上より、4つの角がすべて等しく、4つの辺がすべて等しいので、
四角形\( \ \mathrm{OB_1DB_2} \ \) は 「正方形である」 ことがわかる。
以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。
https://makelemonadejp.com/common-test-for-university-admiss...共有:
プロフィール
Author Profile
