正十二面体とベクトル（その4）【大学入学共通テスト】

2023年3月12日2024年4月9日ベクトル,大学入学共通テスト

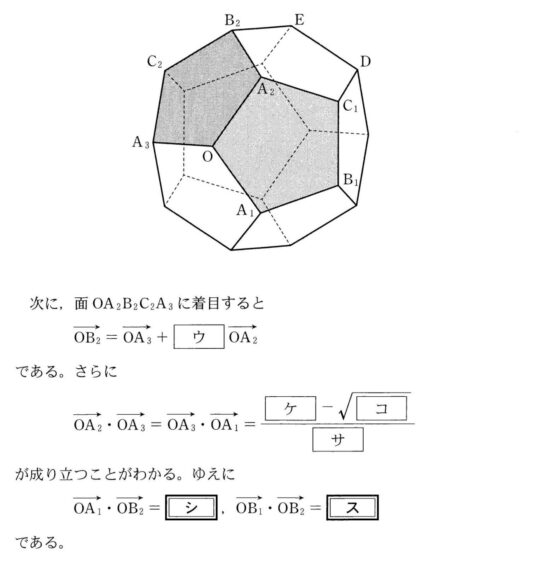
$$\begin{align}\overrightarrow{\mathrm{OA_1}}\cdot \overrightarrow{\mathrm{OB_2}}=&\overrightarrow{\mathrm{OA_1}}\left( \overrightarrow{\mathrm{OA_3}}+a\overrightarrow{\mathrm{OA_2}}\right) \\ =&\overrightarrow{\mathrm{OA_1}}\cdot \overrightarrow{\mathrm{OA_3}}+a\overrightarrow{\mathrm{OA_1}}\cdot \overrightarrow{\mathrm{OA_2}} \\ =&b\left( a+1\right) \\ =&\frac{1-\sqrt{5}}{4}\left( \frac{1+\sqrt{5}+2}{2}\right)\\ =&{\color{#0004fc}{\frac{-1-\sqrt{5}}{4}}}\end{align}$$

$$\begin{align}\overrightarrow{\mathrm{OB_1}}\cdot \overrightarrow{\mathrm{OB_2}}=&\left( \overrightarrow{\mathrm{OA_2}}+a\overrightarrow{\mathrm{OA_1}}\right)\left( \overrightarrow{\mathrm{OA_3}}+a\overrightarrow{\mathrm{OA_2}}\right) \\ =&\overrightarrow{\mathrm{OA_2}}\cdot \overrightarrow{\mathrm{OA_3}}+a\vert \overrightarrow{\mathrm{OA_2}} \vert^2+a\overrightarrow{\mathrm{OA_1}}\cdot \overrightarrow{\mathrm{OA_3}}+a^2\overrightarrow{\mathrm{OA_1}}\cdot \overrightarrow{\mathrm{OA_2}} \\ =&b+a+ab+a^2b\\ =&b\left( a^2+a+1\right)+a\\ =&2\lbrace b\left( a+1\right)\rbrace+a\\ =&2\times \left( \frac{-1-\sqrt{5}}{4}\right)+\frac{1+\sqrt{5}}{2}\\ =&{\color{#0004fc}{0}} \end{align}$$

Lukia

空欄「ス」の値を求める式を展開していくと、
空欄「シ」が活かせるのがわかりますか？
センター試験も共通テストも、誘導のさらに上、超俯瞰で展開のポイントをおさえる力が必要となるといえます。

以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。

大学入学共通テスト2021年数学ⅡBの記事一覧

2021年大学入学共通テストの数学2Bの問題を解いてみました。

 https://makelemonadejp.com/common-test-for-university-admiss...

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。