残存簿価を求めて賢くお買い物をする【ビジネス数学検定2級合格への道】

2022年6月1日2023年1月31日ビジネス数学検定ビジネス数学検定2級

読了時間: 約3分1秒

第75回ビジネス数学検定受検まであと27日
受検勉強を再開した2022年4月18日より45日経過しています。

リサイクルショップはお買い得なのか？

小学二年生の姪っ子が昨年よりピアノを習っています。
いとこから譲り受けたキーボードで練習していたそうですが、いよいよそれも壊れてしまい、
私が使っていた電子ピアノを譲ってもらえないかとの相談がきました。
しかし、その電子ピアノを買ったのが四半世紀前。
さすがに音が出ない鍵盤もあり、これはあきらめてもらうことになりました。

さて、妹（姪っ子の母）が中古の電子ピアノを探してきたのですが、
7年落ちで5万強でした。

電子ピアノの耐用年数は10〜20年と言われていますが、
さすがに20年は言い過ぎなようにも思えますので、まぁ、間を取って15年。
あと8年ぐらいはもってくれるでしょう。
その時、姪っ子は15歳。進路や将来の夢などもある程度具体的になってくる年頃ですから、
そのときに、ピアノとどう関わりたいかで、買い換えるものも変わってくるのではないか。と妹にはアドバイスしました。

ビジネス数学検定で、減価償却についても勉強していたので、
この電子ピアノの減価償却と価格の妥当性について調べてみたくなりました。

減価償却の定率法は平均減少率のこと？

式を見ていくと、どうも幾何平均（相乗平均）を使っていて、
平均増加率ならぬ平均減少率が減価償却の定率にあたるのではないかと思えてきたので、試してみました。

2015年に16万で販売されていた電子ピアノを
2022年に5万で買ったとして、その定率を求めてみます。
$$\begin{align}1-\sqrt[ 7 ]{ \frac{5}{16} }=&1-0.84 \\\\ =&0.16 \end{align}$$ 定率は$ \ 0.16 \ $とわかりました。
ちなみに、2022年現在の残存簿価を求めてみます。
$$\begin{align}16\times \left( 1-0.16\right)^{\left( 2022-2015\right)}=&16\times 0.84^7 \\\\ =&4.72 \end{align}$$
本体価格がたしかこのぐらいで、消費税だの配送料などを含めたら5万強だったので、
妹は妥当な買い物をしたといえますね。

さらに、寿命と仮定している2030年時点の残存簿価も計算してみます。
$$\begin{align}16\times \left( 1-0.16\right)^{\left( 2030-2015\right)}=&16\times 0.84^{15} \\ =&1.17\end{align}$$

もう買い替えと引き換えに無料で引き取ってもらうか、お金を出さないと引き取ってもらえないような残存簿価になっていますね。

Lukia

姪っ子よ！がんばって弾きつぶすのだぞ！(笑)

ちなみに、私の電子ピアノの定率も計算してみると、0.19 でした。
以前、買取業者に問い合わせたら、
「当時の最高モデルを買われてるみたいですが、電子ピアノは家電のようなものなので、10年以上経過すると、引き取るのにお金を出していただかなきゃいけないぐらいなんです。」と言われたことがあります。
実際計算してみると、問い合わせた時点で残存簿価は1万円台になっていました。

定率の求め方を覚えて賢く買い物しよう

減価償却の定率の求め方を覚えておけば、リサイクルショップで売られている家電などが買いなのかそうじゃないのかの判断がつきやすくなりますね。
また、新品を買うにしても、価格を想定する使用年数で単純に割って、「年間○万円ぐらいか〜」と考えますが、これは定額法の考え方ですね。

しかし、買い取る側は、定額法ではなく、よりシビアな定率法で計算しています。
モノは、使用状況や経年で価値が低減していきますので、○万円$ \ \times \ $ 経過年数で考えるのはちょっと都合がよすぎるんでしょうね。
次の買い替え品のための貯金は定額法で考え、使っているモノの価値は、定率法で考えたほうがよさそうです。

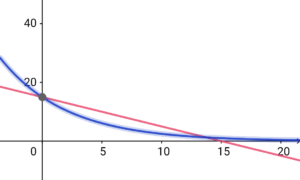
最後に、定額法と定率法での違いを視覚的に示して終わります。

耐用年数15年の商品を15万円で購入したとする。
$ \ x \ $年後の残存簿価を$ \ y \ $とすると、
定額法の場合、残存簿価は、$ \ y=-x+15 \ $で求められる。（下のグラフの赤い直線）
定率法の場合、残存簿価は、$ \ y=15\times 0.835^x \ $で求められる。（下のグラフの青い曲線）