健全な経営には「損益分岐点」が欠かせない?!
読了時間: 約1分42秒
問題
ある通信販売会社は、健康食品を取り扱っている。
健康食品の仕入れ価格は1箱4000円であり、販売価格は6000円である。送料は当社持ちで1箱あたり500円かかる。
また、会社を運営するため家賃や人件費などの固定費は、ひと月あたり300000円かかる。
問1 月間損益分岐点売上高および売上数量をそれぞれ求めよ。
問2 ひと月あたり100000円の利益を確保するのに必要な売上高と売上数量をそれぞれ求めよ。
健康食品の仕入れ価格は1箱4000円であり、販売価格は6000円である。送料は当社持ちで1箱あたり500円かかる。
また、会社を運営するため家賃や人件費などの固定費は、ひと月あたり300000円かかる。
問1 月間損益分岐点売上高および売上数量をそれぞれ求めよ。
問2 ひと月あたり100000円の利益を確保するのに必要な売上高と売上数量をそれぞれ求めよ。
損益分岐点は2つの直線の交点
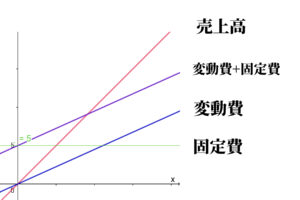損益分岐点は、売上高を表す赤い直線と、変動費+固定費を表す紫の直線の交点です。
売上数量を \( \ x \ \) ,金額を \( \ y \ \) とします。
販売単価を \( \ a \ \) , 一つあたりの変動費を \( \ b \ \) , 固定費を \( \ c \ \) とします。
売上高は \( \ y=ax \ \)
変動費は \( \ y=bx \ \)
固定費は \( \ y=c \ \)
変動費+固定費は \( \ y=bx+c \ \)
さらに、
損益分岐点の数量は、\( \ x=\displaystyle\frac{c}{\left( a-b\right)}=\displaystyle\frac{\rm{固定費}}{\left( \rm{販売単価}-\rm{変動費}\right)} \ \)
利益は、\( \ y=\left( a-b\right)x-c=\left( \rm{販売単価}-\rm{変動費}\right)x-\rm{固定費} \ \) で求められます。
解法
損益分岐点売上高と売上数量を求める
売上高は、\( \ y=0.6x \ \)変動費+固定費は、\( \ y=0.45x+30 \ \) で表される。
損益分岐点の売上数量を\( \ x \ \)とする。
$$\begin{align}0.6x=&0.45x+30 \\\\ 0.15x=&30 \\\\ x=&200\left( \rm{個}\right) \end{align}$$
損益分岐点売上高は、
\( \ 0.6\times 200=120 \ \)（万円）
目標の利益をあげるには？
$$\begin{align}\left( 0.6-0.45\right)x-30 \geqq &10 \\\\ 0.15x-30 \geqq &10 \\\\ 0.15x \geqq &40\\\\ x \geqq &266.6 \end{align}$$ 売上数量は267個売上高は、\( \ 0.6\times 267=160.2 \ \)(万円）
共有:
プロフィール
Author Profile
