自転車で君に追いつきたい。【粗忽な大人、高校入試問題を解く〜それ、誤答です！〜】

2022年4月18日2023年1月9日中学数学

読了時間: 約4分18秒

広島県公立高校入試の2022年、2021年、2020年の数学の問題を解いてみました。
深い読解能力と素早い処理能力が必要とされる問題になっているな。と感じました。
3ヶ年分の問題のうち、私がおっちょこちょいなことをしたり、ツメが甘くて間違えた問題について解き直してみようと思います。

問題

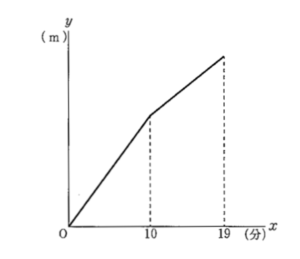
Aさんは駅を出発し、初めの$ \ 10 \ $分間は平らな道を、そのあとの$ \ 9 \ $分間は坂道を歩いて図書館に行きました。下の図は、Aさんが駅を出発してから$ \ x \ $分後の駅からの距離を$ \ y \ $mとし、$ \ x \ $と$ \ y \ $の関係をグラフに表したもので$ \ 10 \leqq x \leqq 19 \ $のときの$ \ y \ $を$ \ x \ $の式で表すと$ \ y=40x+280 \ $です。Bさんは、Aさんが駅を出発した$ \ 8 \ $分後に自転車で駅を出発し、Aさんと同じ道を通って、平らな道、坂道ともに分速$ \ 160 \ $mで図書館に行きました。Bさんはその途中でAさんに追いつきました。BさんがAさんに追いついたのは、駅から何mのところですか。

2021年大問2-(3)

Lukia

ふと思ったこと。
「坂道」には上り坂と下り坂があるのに、私達は無条件に「上り坂」を想定してしまうなぁ。と。そして、問題にあっさり「坂道」と書いてあるのは、作成者も無条件に「上り坂」をイメージしていたからなのかな。と。

（あっさり「坂道」なんてわからない。下り坂だったら、平らな道よりも早く歩けるかもしれないじゃん！）と思うアマノジャクも出てきそうですが、そこはグラフで抑え込むつもりらしい。

グラフを見ると、坂道の傾きは、平らな道のそれよりも緩やかです。ということは、平らな道よりも歩く速度が遅くなっているということなので、やっぱり上り坂を想定しているってことなんでしょうね。

解法

Aさんが坂道を歩き始めるのは、駅から歩き始めて10分後なので、
駅から坂道までの距離（平らな道）は、
$$\begin{align}y=&40\times 10+280 \\\\ =&400+280 \\\\ =&680 \end{align}$$ $ \ 680 \ $mとわかる。

（ちなみに、$ \ 680\div10=68 \ $より、Aさんの平らな道を歩く速度は、分速$ \ 68 \ $mである。）

Lukia

今回の問題で、Aさんが平らな道を歩く速さを求める必要はありません。
しかし、坂道を歩いているときの分速と比べ、グラフの傾きを確認すれば、計算が正しいかどうかの判別ができるため、「ちなみに」として数値を求めています。

Bさんが自転車で平らな道を通り切るには、
$ \ 680\div160=4.25 \ $
4分以上かかる。
つまり、Bさんが平らな道を通りきるのは、Aさんが駅を出発して12分以上あとになるので、
Bさんは、坂道でAさんに追いつくとわかる。

ここで、Bさんが、坂道でAさんに追いつくのにかかった時間（Bさんが自転車で走った時間）を$ \ t \ $分とする。
また、AさんがBさんに追いつかれるまでに歩いた時間は、$ \ x=t+8 \ $と表せる。
ゆえに、$ \ t \ $は、($ \ 10 \leqq t+8 \leqq 19 \ $)を満たす。
BさんがAさんに追いつくということは、「Bさんが駅から自転車で走った距離が、Aさんが駅から歩いた距離に等しい」ということなので、
$$\begin{align}160t=&40\left( t+8\right)+280 \\\\ 160t=&40t+320+280 \\\\ 120t=&600\\\\ t=&5 \end{align}$$ $ \ x=t+8 \ $より、
$ \ x=13 \ $
$$\begin{align}y=&40\times 13+280 \\\\ =&800\end{align}$$ BさんがAさんに追いついたのは、駅から$ \ 800 \ $mのところである。

こたえ

$ \ 800 \ $m

広がる妄想。

数学の文章題の設定は、弟が忘れ物をして、兄がそれを届けに追いかけたり、なぜか池の周りをぐるぐるしたり。
溶かす食塩の量を間違えたり（危険な溶質だったらどうするんだろうとヒヤヒヤします）、
なにしろツッコミどころ満載のものが多いですよね。

今回の問題も、なんで追いつかなきゃいけないんだ！と思ったのですが、この2人の関係性をちょっと妄想してみました。
映画『君の膵臓をたべたい』のキャストをシフトしてみました。
Aさんを、浜辺美波ちゃん、Bさんを北村匠海くんとします。
ふたりは、3学期終了の1週間前に付き合い始めました。

春休み、坂道の上にある桜のきれいな図書館で、宿題をこなしながらの図書館デートです。
美波ちゃんは電車を利用しているので、駅で匠海くんと待ち合わせていました。
ところが、匠海くん、待ち合わせ時間に遅れてしまいます。

美波ちゃんは、しばらく待っていましたが、歩きはじめます。
不動産の徒歩時間が分速80mですから、美波ちゃんの分速68mはゆっくりめですよね。
（来ないなぁ。どうしたのかなぁ。・・・春だ〜。桜、きれいだなぁ。）なんて、来ない匠海くんを振り返りつつ、沿道の桜を眺めながら、ぽてぽて歩いていきます。

美波ちゃんが坂道にさしかかったころ、匠海くんは駅に着きます。
美波ちゃんはいません。680m以上離れているので、姿を確認することもできません。

匠海くん、駅までも全速力で走ってきましたが、あと少し。分速160mで、自転車を漕ぎます。（桜吹雪を巻き上げて？）
そして、数分後、匠海くんは美波ちゃんのぽてぽて歩く姿を見つけます。荷物が重いのか、少し上体を曲げながら、淡い桜色のシフォンスカートをふわふわと揺らして歩いています。

「ごめん！遅くなって！」と匠海くん。
「んもぉ〜、遅いよ〜。」と美波ちゃん。
「荷物、（かごに）入れなよ」と匠海くん。
「ありがと♪」と嬉しそうな美波ちゃん。

匠海くんは自転車を押し、身軽になった美波ちゃんはぴょんぴょん跳ねるように坂道を歩いていくのでした。

と思っていたけど！

問題の設定では、BさんはAさんに追いついてもそのまま走り抜けて図書館に行ってしまうようです。

Lukia

じゃ、AさんとBさんは、少ない自習室の席を争う受験生か？（汗）

殺伐とした人間関係のようでした…。