誘導すらも俯瞰する【大学入学共通テスト】
誘導のさらなる高みから俯瞰する
マークシート形式の数学問題は、
誘導に乗れる・乗れない、誘導者との相性のよしあしによって、
解答の出来具合が変わってきます。
この誘導とうまくつきあえるかどうかは、日頃の訓練の量と質に関わってきますが、
今回問題を解いていて、大事だなぁ。と感じたのは、
誘導のもう一段階、二段階上の高みから俯瞰し、解答の流れを把握する感覚です。
誘導にうまく乗れず、振り回されてはいけませんが、
誘導に乗れたとしても、誘導者と並走するだけでは、これまたうまくいかないように思います。
問題を解く自分、誘導者を見おろす、超越者の視点を持つことです。
誘導者の動きや狙いが把握できれば、問題を解く自分に指示ができますよね。
この視点を持っているから、すごい理系の人たちはぱぱっと解けちゃうのでしょう。
能力は指数関数のようなもの?!
では、この視点、一部の天才しか持てないのか。というと、
そんなことはないと思います。
能力の伸びを、指数関数でたとえてみます。
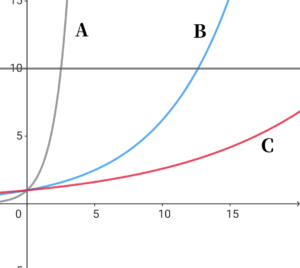今回は、天才Aくんの関数を\( \ y=2.5^x \ \) （灰色の曲線）とし、凡才Bくんの関数を\( \ y=1.2^x \ \) （水色の曲線）とし、
凡才Cくんの関数を\( \ y=1.1^x \ \) （赤い曲線）とします。
そして到達するべき能力の目標値を\( \ y=10 \ \) とします。
Lukia
当初の数字よりかなり大きい数にしました。
そして、指数関数は、底が\( \ 1 \ \)よりちょっとでも大きければ、右上がりに増加していきます。
ちなみに、この「底が\( \ 1 \ \)よりちょっとでも大きければ」というのがミソです。
たとえば、銀行などの預金金利を考えてみてください。
金利\( \ 0.01 \ \)％というと、\( \ 1.00001 \ \)ということになりますが、
これは、\( \ 1 \ \)よりほ〜〜〜〜〜〜〜んのちょっとだけ大きいですね。
しかし、これをあなどってはいけません。
預ける金額が大きければ、
タンス預金をするよりは安全ですし、微々たる額ですが、お金も増えるのです。
そして、そのまま預けておけば、増えた金利も元金となり、お金も増えていきます。
これが、複利のすばらしいところ、おそろしいところです。
急がば回せ
閑話休題。
底をポテンシャルとし、
\( \ x \ \)を回数とします。
まず、グラフを見て驚くのは、BくんとCくんの伸びの違いではないでしょうか。Bくんの底（ポテンシャル）は\( \ 1.2 \ \)で、Cくんのポテンシャルと\( \ 0.1 \ \)しか変わらず、
Cくんの\( \ 1.09 \ \)倍程度なのに、目測で11回から12回ぐらいで目標値に到達しています。
それに対し、Cくんは15回でも目標値に至らず、グラフ画像の見切れたところで目標値に達するものと思われます。
もし、このグラフ画像の右端が、試験日だったとしたら。
Cくんは、能力が十分に高められないまま、試験に臨むことになります。
ポテンシャルが一定だとしても、くりかえせばくりかえすほど、能力は高まっていくことがわかりますし、
能力は高まるんだ！と信じて、くりかえすスパンを短くすれば、Cくんも試験に間に合う可能性が十分にあるのです。
以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。
https://makelemonadejp.com/common-test-for-university-admiss...共有:
プロフィール