大学祭のたこ焼きの損益分岐点売上高は？

2022年6月9日2023年1月31日ビジネス数学検定,中学数学ビジネス数学検定2級

損益分岐点は2つの直線の交点

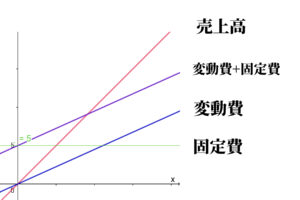損益分岐点は、売上高を表す赤い直線と、変動費+固定費を表す紫の直線の交点です。
売上数量を \( \ x \ \) ,金額を \( \ y \ \) とします。
販売単価を \( \ a \ \) , 一つあたりの変動費を \( \ b \ \) , 固定費を \( \ c \ \) とします。

売上高は \( \ y=ax \ \)
変動費は \( \ y=bx \ \)
固定費は \( \ y=c \ \)
変動費+固定費は \( \ y=bx+c \ \)

さらに、
損益分岐点の数量は、\( \ x=\displaystyle\frac{c}{\left( a-b\right)}=\displaystyle\frac{\rm{固定費}}{\left( \rm{販売単価}-\rm{変動費}\right)} \ \)
利益は、\( \ y=\left( a-b\right)x-c=\left( \rm{販売単価}-\rm{変動費}\right)x-\rm{固定費} \ \) で求められます。

解法

問1 損益分岐点の販売数量は何舟か？

損益分岐点の販売数量を\( \ x \ \)舟とする。
たこ焼きの売上高は、 \( \ y=300x \ \)
変動費+固定費は、\( \ y=150x+75000 \ \) と表せる。
損益分岐点は、売上高と変動費+固定費が等しいときなので、
$$\begin{align}300x=&150x+75000 \\\\ 150x=&75000 \\\\ x=&500 \end{align}$$
\( \ 500 \ \)舟

問2 損益分岐点の売上高は何円か？

問1で求めた販売数量を売上高を表す式に代入する。
\( \ y=300\times 500=150000 \ \)

150,000円

問3 900舟販売した時の利益はいくらか？

利益は、売上高と変動費+固定費の差です。
利益を求める式は、 \( \ y=300x-\left( 150x+75000\right) \ \)
すなわち、\( \ y=150x-75000 \ \) と表せる。
$$\begin{align}x=&900 \ \rm{のとき} \\\\ y=&150\times 900-75000 \\\\ =&60000 \end{align}$$ 60,000円

問4 45,000円の利益を獲得するためには何舟販売する必要があるか?

$$\begin{align}45000=&150x-75000 \\\\ x=&800 \end{align}$$
800個

Leave This Blank:Leave This Blank Too:Do Not Change This:

メールアドレス：

 

よろしければ,アンケートに御協力ください。
アンケートでは、お読みになったタイトルをうかがいますので、御確認ください。
この記事のタイトルは『大学祭のたこ焼きの損益分岐点売上高は？』です。