「平面ベクトルの内分比からcosθの大きさを求める」問題を解いてみる。【たすきがけで比を統一せよ!!】
する点を\( \ \mathrm{C} \ \), 辺\( \ \mathrm{OB} \ \)を\( \ 1:2 \ \)に内分する点
を\( \ \mathrm{D} \ \), 直線\( \ \mathrm{AD} \ \),\( \ \mathrm{BC} \ \)の交点を\( \ \mathrm{P} \ \)とする。
このとき、 \( \ \vert \mathrm{OA} \vert=2 \ \) , \( \ \vert \mathrm{OB} \vert=3 \cos \angle \mathrm{AOB}=\displaystyle\frac{1}{6} \ \) , \( \ \vert \mathrm{OP} \vert=\displaystyle\frac{9}{7} \ \)である。 \( \ \cos \angle \mathrm{AOP} \ \)の値を求めよ。
解法
直線\( \ \mathrm{OP} \ \)と辺\( \ \mathrm{AB} \ \)の交点を\( \ \mathrm{E} \ \)とする。
三角形\( \ \mathrm{OAB} \ \)とその内分線の関係は以下の図の通り。
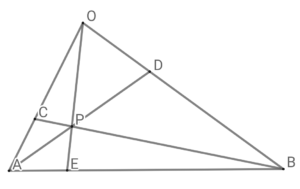
内分比は以下の図の青い数字のとおりとなる。
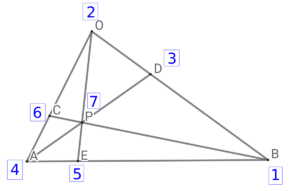
\( \ \cos \angle \mathrm{AOP}=\displaystyle\frac{\overrightarrow{\mathrm{OC}}\cdot \overrightarrow{\mathrm{OP}}}{\vert \overrightarrow{\mathrm{OC}} \vert\vert \overrightarrow{\mathrm{OP}} \vert} \ \)
\( \ \begin{eqnarray} \left\{ \begin{array}{l} \overrightarrow{\mathrm{OC}}=\displaystyle\frac{2}{3}\overrightarrow{\mathrm{OA}} \ , \ \vert \overrightarrow{\mathrm{OC}} \vert=\displaystyle\frac{4}{3} \\ \overrightarrow{\mathrm{OP}}=\displaystyle\frac{1}{7}\left( 4\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}\right) \ , \ \vert \overrightarrow{\mathrm{OP}} \vert=\displaystyle\frac{9}{7} \end{array} \right. \end{eqnarray} \ \) $$\begin{align}\cos \angle \mathrm{AOP}=&\frac{\displaystyle\frac{2}{3}\overrightarrow{\mathrm{OA}}\times \displaystyle\frac{1}{7}\left( 4\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}\right)}{\displaystyle\frac{4}{3}\times \displaystyle\frac{9}{7}} \\\\ =&\frac{1}{18}\left( 4\vert \overrightarrow{\mathrm{OA}} \vert^2+\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}\right) \\\\ \rm{ここで}&\\\\ \cos \angle \mathrm{AOB}=&\frac{\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}}{\vert \overrightarrow{\mathrm{OA}} \vert\vert \overrightarrow{\mathrm{OB}} \vert}=\frac{1}{6}\\\\ &\frac{\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}}{2\times 3}=\frac{1}{6}\\\\ &\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=1 \ \rm{より}\\\\ \cos \angle \mathrm{AOP}=&\frac{1}{18}\left( 4\cdot 2^2+1\right)\\\\ =&\frac{17}{18} \end{align}$$
こたえ
\( \ \cos \angle \mathrm{AOP}=\displaystyle\frac{17}{18} \ \)
以下の記事一覧に他のボリュームのブログカードを載せています。途中のボリュームからお読みになった方はこちらからどうぞ。
https://makelemonadejp.com/plane-vector-internal-division-of...共有:
プロフィール
