税込価格から定価を求める【税込価格から定価と税額を求めよう】
それでは、 今回からいよいよ税込価格から定価と税額を求めていきます。
インボイス制度に関わる人は、 何度か読み返してください。
平屋から2階建てで示すよ
前回までで、
消費税率が10％のとき、その税額は、定価を10等分したうちの1つ分に相当するので、
税込価格は、 定価×1.1で求められるとお話ししました。
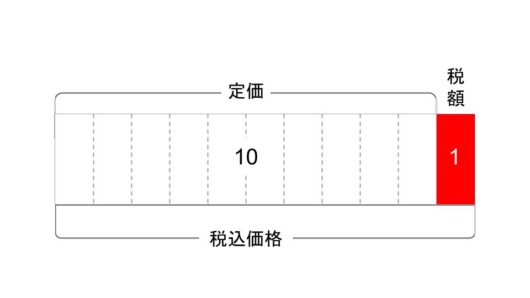
今回は、 定価、 税額、 税込価格の図を2階建てで表してみます。
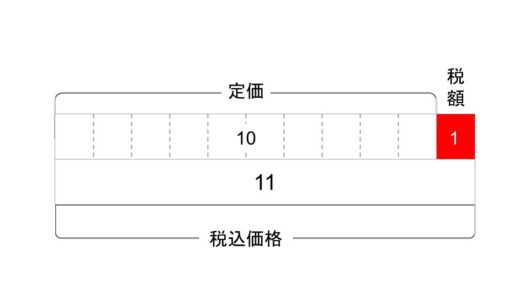
2階建てにすると分数に見えてきませんか？
定価は、 税込価格を11等分したとき、 その10個分に相当します。
また税額は、 税込価格を11等分したその1つ分に相当します。
さらに、 定価と税額は、 10：1の関係になっていることに気づけましたか？
定価の\( \ \displaystyle\frac{1}{10} \ \)、 すなわち、定価を\( \ 10 \ \)で割れば、税額が求められるということになります。
$$\begin{align}\frac{1}{11}\times 10\times \frac{1}{10}=&\frac{10}{11\times 10} \\ =&\frac{1}{11} \end{align}$$
税込価格から定価を求める公式
今回は、 税込価格から定価を求める練習をしましょう。
これまで、ひとまとまりのものを等分にする。という感覚を身に着けてほしかったので、
分数を用いて説明してきましたが、
分数は、 電卓で表しにくいので、 もう少し変形してみようと思います。
しばらく、こちゃこちゃと変形しますが、
難しい人は、一番最後に「税込価格から定価を求める」公式を示しますので、
ここはぼんやり見ていてください。
$$\begin{align}\frac{10}{11}\times 10=&\frac{10}{11} \\ =&\frac{10\div10}{11\div10} \\ =&\frac{1}{1.1} \end{align}$$
では、 税込価格が\( \ t \ \)のとき定価\( \ x \ \)はいくらか。
\( \ x=t\times \displaystyle\frac{1}{1.1} \ \)
\( \ x=t\div1.1 \ \)
で求められることになります。
練習問題
それでは、6つ練習問題を出します。
電卓片手に計算してみてください。
答えは、まとめて示しますので、
メモしておいてくださいね。
第1問
定価（\( \ x \ \)）はいくらか。
第2問
定価（\( \ x \ \)）はいくらか。
第3問
定価（\( \ x \ \)）はいくらか。
第4問
定価（\( \ x \ \)）はいくらか。
第5問
定価（\( \ x \ \)）はいくらか。
第6問
定価（\( \ x \ \)）はいくらか。
答え
第1問
定価：100円
第2問
定価：250円
第3問
定価：120円
第4問
定価：10,000円
第1問
定価：3,650円
第1問
定価：98,000円
油断するなよ?!
今回は、「定価を求めたいなら、税込価格を1.1で割ればいい」というのが、わかっていただければ十分です。
次回、もう少し実践的な内容に入りますので、
公式と電卓操作をしっかり覚えておいてください。
それでは、今回はここまで。
以下の記事一覧に他のボリュームのブログカードを載せています。
途中のボリュームからお読みになった方はこちらからどうぞ。
https://makelemonadejp.com/calculate-the-list-price-and-tax-...共有:
プロフィール
